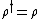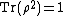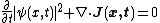1. Formalism
     Kinematical postulates   Dynamics  Dynamics related to single particle in a potential / other spatial properties   Measurement postulates    Indistinguishable particles    Quantum statistical mechanics  

2. Nonlocality

3. Rotation: spin/angular momentum

4. Approximation methods

5. Historical Terms / semi-classical treatment

6. Uncategorized terms

7. See also

8. Notes

9. References

This is a glossary for the terminology often encountered in undergraduate quantum mechanics courses.

• Different authors may have different definitions for the same term.
• The discussions are restricted to Schrödinger picture and non-relativistic quantum mechanics.
• Notation:
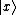  • - position eigenstate
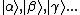  • - wave function of the state of the system
  • - total wave function of a system
  • - wave function of a system (maybe a particle)
  • - wave function of a particle in position representation, equal to

Formalism

Kinematical postulates

a complete set of wave functions

A basis of the Hilbert space of wave functions with respect to a system.

bra

The Hermitian conjugate of a ket is called a bra. . See "bra–ket notation".

//Bra–ket notation">Bra–ket notation

The bra–ket notation is a way to represent the states and operators of a system by angle brackets and vertical bars, for example, and .

//Density matrix">Density matrix

Physically, the density matrix is a way to represent pure states and mixed states. The density matrix of pure state whose ket is is .

Mathematically, a density matrix has to satisfy the following conditions:

Density operator

Synonymous to "density matrix".

Dirac notation

Synonymous to "bra–ket notation".

//Hilbert space">Hilbert space

Given a system, the possible pure state can be represented as a vector in a Hilbert space. Each ray (vectors differ by phase and magnitude only) in the corresponding Hilbert space represent a state.^[1]

Ket

A wave function expressed in the form is called a ket. See "bra–ket notation".

//Mixed state (physics)">Mixed state

A mixed state is a statistical ensemble of pure state.

criterion:

Pure state:

Mixed state:

Normalizable wave function

A wave function is said to be normalizable if . A normalizable wave function can be made to be normalized by .

Normalized wave function

A wave function is said to be normalized if .

//Pure state">Pure state

A state which can be represented as a wave function / ket in Hilbert space / solution of Schrödinger equation is called pure state. See "mixed state".

//Quantum numbers">Quantum numbers

a way of representing a state by several numbers, which corresponds to a complete set of commuting observables.

A common example of quantum numbers is the possible state of an electron in a central potential: , which corresponds to the eigenstate of observables (in terms of ), (magnitude of angular momentum), (angular momentum in -direction), and .

Spin wave function

Part of a wave function of particle(s). See "total wave function of a particle".

Spinor

Synonymous to "spin wave function".

Spatial wave function

Part of a wave function of particle(s). See "total wave function of a particle".

//Quantum state">State

A state is a complete description of the observable properties of a physical system.

Sometimes the word is used as a synonym of "wave function" or "pure state".

State vector

synonymous to "wave function".

//Statistical ensemble (mathematical physics)">Statistical ensemble

A large number of copies of a system.

//Physical system">System

A sufficiently isolated part in the universe for investigation.

//Tensor product">Tensor product of Hilbert space

When we are considering the total system as a composite system of two subsystems A and B, the wave functions of the composite system are in a Hilbert space , if the Hilbert space of the wave functions for A and B are and respectively.

Total wave function of a particle

For single-particle system, the total wave function of a particle can be expressed as a product of spatial wave function and the spinor. The total wave functions are in the tensor product space of the Hilbert space of the spatial part (which is spanned by the position eigenstates) and the Hilbert space for the spin.

Wave function

The word "wave function" could mean one of following:

1. A vector in Hilbert space which can represent a state; synonymous to "ket" or "state vector".
2. The state vector in a specific basis. It can be seen as a covariant vector in this case.
3. The state vector in position representation, e.g. 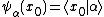, where 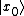is the position eigenstate.

Dynamics

Degeneracy

See "degenerate energy level".

Degenerate energy level

If the energy of different state (wave functions which are not scalar multiple of each other) is the same, the energy level is called degenerate.

There is no degeneracy in 1D system.

Energy spectrum

The energy spectrum refers to the possible energy of a system.

For bound system (bound states), the energy spectrum is discrete; for unbound system (scattering states), the energy spectrum is continuous.

related mathematical topics: Sturm–Liouville equation

//Hamiltonian (quantum mechanics)">Hamiltonian

The operator represents the total energy of the system.

//Schrödinger equation">Schrödinger equation

-- (1)

(1) is sometimes called "Time-Dependent Schrödinger equation" (TDSE).

Time-Independent Schrödinger Equation (TISE)

A modification of the Time-Dependent Schrödinger equation as an eigenvalue problem. The solutions are energy eigenstate of the system.

-- (2)

Dynamics related to single particle in a potential / other spatial properties

In this situation, the SE is given by the form

It can be derived from (1) by considering and

Bound state

A state is called bound state if its position probability density at infinite tends to zero for all the time. Roughly speaking, we can expect to find the particle(s) in a finite size region with certain probability. More precisely, when , for all .

There is a criterion in terms of energy:

Let be the expectation energy of the state. It is a bound state iff .

Position representation and momentum representation

Position representation of a wave function: ,

momentum representation of a wave function: ;

where is the position eigenstate and the momentum eigenstate respectively.

The two representations are linked by Fourier transform.

Probability amplitude

A probability amplitude is of the form .

//Probability current">Probability current

Having the metaphor of probability density as mass density, then probability current is the current:

The probability current and probability density together satisfy the continuity equation:

//Probability amplitude">Probability density

Given the wave function of a particle, is the probability density at position and time . means the probability of finding the particle near .

Scattering state

The wave function of scattering state can be understood as a propagating wave. See also "bound state".

There is a criterion in terms of energy:

Let be the expectation energy of the state. It is a scattering state iff .

Square-integrable

Square-integrable is a necessary condition for a function being the position/momentum representation of a wave function of a bound state of the system.

Given the position representation of a state vector of a wave function, square-integrable means:

1D case: .

3D case: .

Stationary state

A stationary state of a bound system is an eigenstate of Hamiltonian operator. Classically, it corresponds to standing wave. It is equivalent to the following things:^[2]

• an eigenstate of the Hamiltonian operator
• an eigenfunction of Time-Independent Schrödinger Equation
• a state of definite energy
• a state which "every expectation value is constant in time"
• a state whose probability density () does not change with respect to time, i.e.

Measurement postulates

//Born's rule">Born's rule

The probability of the state collapse to an eigenstate of an observable is given by .

//Collapse postulate">Collapse

"Collapse" means the sudden process which the state of the system will "suddenly" change to an eigenstate of the observable during measurement.

//Eigenstates">Eigenstates

An eigenstate of an operator is a vector satisfied the eigenvalue equation: , where is a scalar.

Usually, in bra–ket notation, the eigenstate will be represented by its corresponding eigenvalue if the corresponding observable is understood.

//Expectation value">Expectation value

The expectation value of the observable M with respect to a state is the average outcome of measuring with respect to an ensemble of state .

can be calculated by:

.

If the state is given by a density matrix , .

//Hermitian operator">Hermitian operator

An operator satisfying .

Equivalently, for all allowable wave function .

//Observable">Observable

Mathematically, it is represented by a Hermitian operator.

Indistinguishable particles

Exchange

Intrinsically identical particles

If the intrinsic properties (properties that can be measured but are independent of the quantum state, e.g. charge, total spin, mass) of two particles are the same, they are said to be (intrinsically) identical.

//Indistinguishable particles">Indistinguishable particles

If a system shows measurable differences when one of its particles is replaced by another particle, these two particles are called distinguishable.

//Boson">Bosons

Bosons are particles with integer spin (s = 0, 1, 2, ... ). They can either be elementary (like photons) or composite (such as mesons, nuclei or even atoms). There are five known elementary bosons: the four force carrying gauge bosons γ (photon), g (gluon), Z (Z boson) and W (W boson), as well as the Higgs boson.

//Fermion">Fermions

Fermions are particles with half-integer spin (s = 1/2, 3/2, 5/2, ... ). Like bosons, they can be elementary or composite particles. There are two types of elementary fermions: quarks and leptons, which are the main constituents of ordinary matter.

//Anti-symmetrization">Anti-symmetrization of wave functions

//Symmetrization">Symmetrization of wave functions

//Pauli exclusion principle">Pauli exclusion principle

Quantum statistical mechanics

//Bose–Einstein distribution">Bose–Einstein distribution

//Bose–Einstein condensation">Bose–Einstein condensation

Bose–Einstein condensation state (BEC state)

Fermi energy

//Fermi–Dirac distribution">Fermi–Dirac distribution

//Slater determinant">Slater determinant

Nonlocality

//Quantum entanglement">Entanglement

//Bell's inequality">Bell's inequality

//Entangled state">Entangled state

//separable state">separable state

//no cloning theorem">no cloning theorem

Rotation: spin/angular momentum

//spin (physics)">Spin

//angular momentum">angular momentum

//Clebsch–Gordan coefficients">Clebsch–Gordan coefficients

//singlet state">singlet state and triplet state

Approximation methods

//adiabatic approximation">adiabatic approximation

//Born–Oppenheimer approximation">Born–Oppenheimer approximation

//WKB approximation">WKB approximation

//time-dependent perturbation theory">time-dependent perturbation theory

//time-independent perturbation theory">time-independent perturbation theory

Historical Terms / semi-classical treatment

//Ehrenfest theorem">Ehrenfest theorem

A theorem connecting the classical mechanics and result derived from Schrödinger equation.

//first quantization">first quantization

//wave–particle duality">wave–particle duality

Uncategorized terms

//uncertainty principle">uncertainty principle

//Canonical commutation relations">Canonical commutation relations

//path integral formulation">Path integral

//wavenumber">wavenumber

See also

• Mathematical formulations of quantum mechanics
• List of mathematical topics in quantum theory
• List of quantum-mechanical potentials
• Introduction to quantum mechanics

Notes

References

• St Michael's Academy, Kilwinning
• St. Michael's Arena
• St. Michael's, Bath
• St Michael's, Bath
• St. Michael's Buzzers
• St Michael's Camden Town
• St Michael's Castle
• St. Michael's Cathedral, Belgrade
• St. Michael's Cathedral (Sitka, Alaska)
• St. Michael's Cathedral (Springfield, Massachusetts)
• St. Michael's Cathedral, Toronto
• St. Michael's Catholic Church, Sharjah
• St Michael's Catholic Grammar School
• St. Michael's Catholic Grammer School
• St Michael's Catholic School, High Wycombe
• St. Michael's Catholic Secondary School
• St. Michael School
• St. Michael School (Frostburg, Maryland)
• St. Michaels Church
• St Michael's Church
• St. Michael's Church
• St Michaels Church
• St Michael's Church, Baddiley
• St Michael's Church, Basingstoke
• St Michael's Church, Bath