- Glossary
- Symbols introduced in Principia Mathematica volume I
- Symbols introduced in Principia Mathematica volume II
- Symbols introduced in Principia Mathematica volume III
- See also
- Notes
- References
- External links
This is a list of the notation used in Alfred North Whitehead and Bertrand Russell's Principia Mathematica (1910–13).
The second (but not the first) edition of volume I has a list of notation used at the end.
Glossary
This is a glossary of some of the technical terms in Principia Mathematica that are no longer widely used or whose meaning has changed.
{{term|apparent variable}}{{defn|bound variable}}{{term|atomic proposition}}{{defn|A proposition of the form R(x,y,...) where R is a relation.}}{{term|Barbara}}{{defn|A mnemonic for a certain syllogism.}}{{term|class}}{{defn|A subset of the members of some type}}{{term|codomain}}{{defn|The codomain of a relation R is the class of y such that xRy for some x.}}{{term|compact}}{{defn|A relation R is called compact if whenever xRz there is a y with xRy and yRz}}{{term|concordant}}{{defn|A set of real numbers is called concordant if all nonzero members have the same sign}}{{term|connected}}{{term|connexity}}{{defn|A relation R is called connected if for any 2 distinct members x, y either xRy or yRx.}}{{term|continuous}}{{defn|A continuous series is a complete totally ordered set isomorphic to the reals. *275}}{{term|correlator}}{{defn|bijection}}{{term|couple}}{{defn|no=1|A cardinal couple is a class with exactly two elements}}{{defn|no=2|An ordinal couple is an ordered pair (treated in PM as a special sort of relation)}}{{term|Dedekindian}}{{defn|complete (relation) *214}}{{term|definiendum}}{{defn|The symbol being defined}}{{term|definiens}}{{defn|The meaning of something being defined}}{{term|derivative}}{{defn|A derivative of a subclass of a series is the class of limits of non-empty subclasses}}{{term|description}}{{defn|A definition of something as the unique object with a given property}}{{term|descriptive function}}{{defn|A function taking values that need not be truth values, in other words what is not called just a function.}}{{term|diversity}}{{defn|The inequality relation}}{{term|domain}}{{defn|The domain of a relation R is the class of x such that xRy for some y.}}{{term|elementary proposition}}{{defn|A proposition built from atomic propositions using "or" and "not", but with no bound variables}}{{term|Epimenides}}{{defn|Epimenides was a legendary Cretan philosopher}}{{term|existent}}{{defn|non-empty}}{{term|extensional function}}{{defn|A function whose value does not change if one of its arguments is changed to something equivalent.}}{{term|field}}{{defn|The field of a relation R is the union of its domain and codomain}}{{term|first-order}}{{defn|A first-order proposition is allowed to have quantification over individuals but not over things of higher type.}}{{term|function}}{{defn|This often means a propositional function, in other words a function taking values "true" or "false". If it takes other values it is called a "descriptive function". PM allows two functions to be different even if they take the same values on all arguments.}}{{term|general proposition}}{{defn|A proposition containing quantifiers}}{{term|generalization}}{{defn|Quantification over some variables}}{{term|homogeneous}}{{defn|A relation is called homogeneous if all arguments have the same type.}}{{term|individual}}{{defn|An element of the lowest type under consideration}}{{term|inductive}}{{defn|Finite, in the sense that a cardinal is inductive if it can be obtained by repeatedly adding 1 to 0. *120}}{{term|intensional function}}{{defn|A function that is not extensional.}}{{term|logical}}{{defn|no=1|The logical sum of two propositions is their logical disjunction}}{{defn|no=2|The logical product of two propositions is their logical conjunction}}{{term|matrix}}{{defn|A function with no bound variables. *12}}{{term|median}}{{defn|A class is called median for a relation if some element of the class lies strictly between any two terms. *271}}{{term|member}}{{defn|element (of a class)}}{{term|molecular proposition}}{{defn|A proposition built from two or more atomic propositions using "or" and "not"; in other words an elementary proposition that is not atomic.}}{{term|null-class}}{{defn|A class containing no members}}{{term|predicative}}{{defn|A century of scholarly discussion has not reached a definite consensus on exactly what this means, and Principia Mathematica gives several different explanations of it that are not easy to reconcile. See the introduction and *12. *12 says that a predicative function is one with no apparent (bound) variables, in other words a matrix.}}{{term|primitive proposition}}{{defn|A proposition assumed without proof}}{{term|progression}}{{defn|A sequence (indexed by natural numbers)}}{{term|rational}}{{defn|A rational series is an ordered set isomorphic to the rational numbers}}{{term|real variable}}{{defn|free variable}}{{term|referent}}{{defn|The term x in xRy}}{{term|reflexive}}{{defn|infinite in the sense that the class is in one-to-one correspondence with a proper subset of itself (*124)}}{{term|relation}}{{defn|A propositional function of some variables (usually two). This is similar to the current meaning of "relation".}}{{term|relative product}}{{defn|The relative product of two relations is their composition}}{{term|relatum}}{{defn|The term y in xRy}}{{term|scope}}{{defn|The scope of an expression is the part of a proposition where the expression has some given meaning (chapter III)}}{{term|Scott}}{{defn|Sir Walter Scott, author of Waverley.}}{{term|second-order}}{{defn|A second order function is one that may have first-order arguments}}{{term|section}}{{defn|A section of a total order is a subclass containing all predecessors of its members.}}{{term|segment}}{{defn|A subclass of a totally ordered set consisting of all the predecessors of the members of some class}}{{term|selection}}{{defn|A choice function: something that selects one element from each of a collection of classes.}}{{term|sequent}}{{defn|A sequent of a class α in a totally ordered class is a minimal element of the class of terms coming after all members of α. (*206)}}{{term|serial relation}}{{defn|A total order on a class[1]}}{{term|significant}}{{defn|well-defined or meaningful}}{{term|similar}}{{defn|of the same cardinality}}{{term|stretch}}{{defn|A convex subclass of an ordered class}}{{term|stroke}}{{defn|The Sheffer stroke (only used in the second edition of PM)}}{{term|type}}{{defn|As in type theory. All objects belong to one of a number of disjoint types.}}{{term|typically}}{{defn|Relating to types; for example, "typically ambiguous" means "of ambiguous type".}}{{term|unit}}{{defn|A unit class is one that contains exactly one element}}{{term|universal}}{{defn|A universal class is one containing all members of some type}}{{term|vector}}{{defn|no=1|Essentially an injective function from a class to itself (for example, a vector in a vector space acting on an affine space)}}{{defn|no=2|A vector-family is a non-empty commuting family of injective functions from some class to itself (VIB)}}Symbols introduced in Principia Mathematica volume I
| Symbol | Approximate meaning | Reference |
|---|---|---|
| ✸ | Indicates that the following number is a reference to some proposition | |
| α,β,γ,δ,λ,κ, μ | Classes | Chapter I page 5 |
| f,g,θ,φ,χ,ψ | Variable functions (though θ is later redefined as the order type of the reals) | Chapter I page 5 |
| a,b,c,w,x,y,z | Variables | Chapter I page 5 |
| p,q,r | Variable propositions (though the meaning of p changes after section 40). | Chapter I page 5 |
| P,Q,R,S,T,U | Relations | Chapter I page 5 |
| . : :. :: | Dots used to indicate how expressions should be bracketed, and also used for logical "and". | Chapter I, Page 10 |
 | Indicates (roughly) that x is a bound variable used to define a function. Can also mean (roughly) "the set of x such that...". | Chapter I, page 15 |
| ! | Indicates that a function preceding it is first order | Chapter II.V |
| ⊦ | Assertion: it is true that | *1(3) |
| ~ | Not | *1(5) |
| ∨ | Or | *1(6) |
| ⊃ | (A modification of Peano's symbol Ɔ.) Implies | *1.01 |
| = | Equality | *1.01 |
| Df | Definition | *1.01 |
| Pp | Primitive proposition | *1.1 |
| Dem. | Short for "Demonstration" | *2.01 |
| . | Logical and | *3.01 |
| p⊃q⊃r | p⊃q and q⊃r | *3.02 |
| ≡ | Is equivalent to | *4.01 |
| p≡q≡r | p≡q and q≡r | *4.02 |
| Hp | Short for "Hypothesis" | *5.71 |
| (x) | For all x This may also be used with several variables as in 11.01. | *9 |
| (∃x) | There exists an x such that. This may also be used with several variables as in 11.03. | *9, *10.01 |
| ≡x, ⊃x | The subscript x is an abbreviation meaning that the equivalence or implication holds for all x. This may also be used with several variables. | *10.02, *10.03, *11.05. |
| = | x=y means x is identical with y in the sense that they have the same properties | *13.01 |
| ≠ | Not identical | *13.02 |
| x=y=z | x=y and y=z | *13.3 |
| ℩ | This is an upside-down iota (unicode U+2129). ℩x means roughly "the unique x such that...." | *14 |
| [] | *14.01 | |
| E! | There exists a unique... | *14.02 |
| ε | A Greek epsilon, abbreviating the Greek word ἐστί meaning "is". It is used to mean "is a member of" or "is a" | *20.02 and Chapter I page 26 |
| Cls | Short for "Class". The 2-class of all classes | *20.03 |
| , | Abbreviation used when several variables have the same property | *20.04, *20.05 |
| ~ε | Is not a member of | *20.06 |
| Prop | Short for "Proposition" (usually the proposition that one is trying to prove). | Note before *2.17 |
| Rel | The class of relations | *21.03 |
| ⊂ ⪽ | Is a subset of (with a dot for relations) | *22.01, *23.01 |
| ∩ ⩀ | Intersection (with a dot for relations). α∩β∩γ is defined to be (α∩β)∩γ and so on. | *22.02, *22.53, *23.02, *23.53 |
| ∪ ⨄ | Union (with a dot for relations) α∪β∪γ is defined to be (α∪β)∪γ and so on. | 22.03, *22.71, *23.03, *23.71 |
| − ∸ | Complement of a class or difference of two classes (with a dot for relations) | *22.04, *22.05, *23.04, *23.05 |
| V ⩒ | The universal class (with a dot for relations) | *24.01 |
| Λ ⩑ | The null or empty class (with a dot for relations) | 24.02 |
| ∃! | The following class is non-empty | *24.03 |
| ‘ | R ‘ y means the unique x such that xRy | *30.01 |
| Cnv | Short for converse. The converse relation between relations | *31.01 |
| Ř | The converse of a relation R | *31.02 |
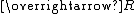 | A relation such that 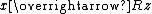 if x is the set of all y such that if x is the set of all y such that 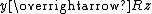 | *32.01 |
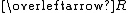 | Similar to 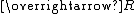 with the left and right arguments reversed with the left and right arguments reversed | *32.02 |
| sg | Short for "sagitta" (Latin for arrow). The relation between 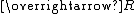 and R. and R. | *32.03 |
| gs | Reversal of sg. The relation between 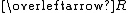 and R. and R. | 32.04 |
| D | Domain of a relation (αDR means α is the domain of R). | *33.01 |
| D | (Upside down D) Codomain of a relation | *33.02 |
| C | (Initial letter of the word "campus", Latin for "field".) The field of a relation, the union of its domain and codomain | *32.03 |
| F | The relation indicating that something is in the field of a relation | *32.04 |
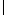 | The composition of two relations. Also used for the Sheffer stroke in *8 appendix A of the second edition. | *34.01 |
| R2, R3 | Rn is the composition of R with itself n times. | *34.02, *34.03 |
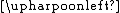 | 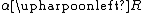 is the relation R with its domain restricted to α is the relation R with its domain restricted to α | *35.01 |
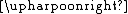 | 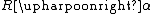 is the relation R with its codomain restricted to α is the relation R with its codomain restricted to α | *35.02 |
 | Roughly a product of two sets, or rather the corresponding relation | *35.04 |
| ⥏ | P⥏α means 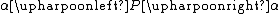 . The symbol is unicode U+294F . The symbol is unicode U+294F | *36.01 |
| “ | (Double open quotation marks.) R“α is the domain of a relation R restricted to a class α | *37.01 |
| Rε | αRεβ means "α is the domain of R restricted to β" | *37.02 |
| ‘‘‘ | (Triple open quotation marks.) αR‘‘‘κ means "α is the domain of R restricted to some element of κ" | *37.04 |
| E!! | Means roughly that a relation is a function when restricted to a certain class | *37.05 |
| ♀ | A generic symbol standing for any functional sign or relation | *38 |
| ” | Double closing quotation mark placed below a function of 2 variables changes it to a related class-valued function. | *38.03 |
| p | The intersection of the classes in a class. (The meaning of p changes here: before section 40 p is a propositional variable.) | *40.01 |
| s | The union of the classes in a class | *40.02 |
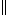 | 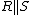 applies R to the left and S to the right of a relation applies R to the left and S to the right of a relation | *43.01 |
| I | The equality relation | *50.01 |
| J | The inequality relation | *50.02 |
| ι | Greek iota. Takes a class x to the class whose only element is x. | *51.01 |
| 1 | The class of classes with one element | *52.01 |
| 0 | The class whose only element is the empty class. With a subscript r it is the class containing the empty relation. | *54.01, *56.03 |
| 2 | The class of classes with two elements. With a dot over it, it is the class of ordered pairs. With the subscript r it is the class of unequal ordered pairs. | *54.02, *56.01, *56.02 |
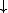 | An ordered pair | *55.01 |
| Cl | Short for "class". The powerset relation | *60.01 |
| Cl ex | The relation saying that one class is the set of non-empty classes of another | *60.02 |
| Cls2, Cls3 | The class of classes, and the class of classes of classes | *60.03, *60.04 |
| Rl | Same as Cl, but for relations rather than classes | *61.01, *61.02, *61.03, *61.04 |
| ε | The membership relation | *62.01 |
| t | The type of something, in other words the largest class containing it. t may also have further subscripts and superscripts. | *63.01, *64 |
| t0 | The type of the members of something | *63.02 |
| αx | the elements of α with the same type as x | *65.01 *65.03 |
| α(x) | The elements of α with they type of the type of x. | *65.02 *65.04 |
| → | α→β is the class of relations such that the domain of any element is in α and the codomian is in β. | *70.01 |
| sm}} | Short for "similar". The class of bijections between two classes | *73.01 |
| sm | Similarity: the relation that two classes have a bijection between them | *73.02 |
| PΔ | λPΔκ means that λ is a selection function for P restricted to κ | *80.01 |
| excl | Refers to various classes being disjoint | *84 |
| ↧ | P↧x is the subrelation of P of ordered pairs in P whose second term is x. | *85.5 |
| Rel Mult | The class of multipliable relations | *88.01 |
| Cls2 Mult | The multipliable classes of classes | *88.02 |
| Mult ax | The multiplicative axiom, a form of the axiom of choice | *88.03 |
| R* | The transitive closure of the relation R | *90.01 |
| Rst, Rst | A relations saying one relation is a positive power of R times another | *91.01, *91.02 |
| Pot | (Short for the Latin word "potentia" meaning power.) The positive powers of a relation | *91.03 |
| Potid | ("Pot" for "potentia" + "id" for "identity".) The positive or zero powers of a relation | *91.04 |
| Rpo | The union of the positive power of R | *91.05 |
| B | Stands for "Begins". Something is in the domain but not the range of a relation | *93.01 |
| min, max | used to mean that something is a minimal or maximal element of some class with respect to some relation | *93.02 *93.021 |
| gen | The generations of a relation | *93.03 |
| ✸ | P✸Q is a relation corresponding to the operation of applying P to the left and Q to the right of a relation. This meaning is only used in *95 and the symbol is defined differently in *257. | *95.01 |
| Dft | Temporary definition (followed by the section it is used in). | *95 footnote |
| IR,JR | Certain subsets of the images of an element under repeatedly applying a function R. Only used in *96. | *96.01, *96.02 |
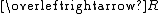 | The class of ancestors and descendants of an element under a relation R | *97.01 |
Symbols introduced in Principia Mathematica volume II
| Symbol | Approximate meaning | Reference |
|---|---|---|
| Nc | The cardinal number of a class | *100.01,*103.01 |
| NC | The class of cardinal numbers | *100.02, *102.01, *103.02,*104.02 |
| μ(1) | For a cardinal μ, this is the same cardinal in the next higher type. | *104.03 |
| μ(1) | For a cardinal μ, this is the same cardinal in the next lower type. | *105.03 |
| + | The disjoint union of two classes | *110.01 |
| +c | The sum of two cardinals | *110.02 |
| Crp | Short for "correspondence". | *110.02 |
| ς | (A Greek sigma used at the end of a word.) The series of segments of a series; essentially the completion of a totally ordered set | *212.01 |
Symbols introduced in Principia Mathematica volume III
| Symbol | Approximate meaning | Reference |
|---|---|---|
| Bord | Abbreviation of "bene ordinata" (Latin for well-ordered), the class of well-founded relations | *250.01 |
| Ω | The class of well ordered relations[2] | 250.02 |
See also
- Glossary of set theory
Notes
1. ^PM insists that this class must be the field of the relation, resulting in the bizarre convention that the class cannot have exactly one element.
2. ^Note that by convention PM does not allow well-orderings on a class with 1 element.
2. ^Note that by convention PM does not allow well-orderings on a class with 1 element.
References
- Whitehead, Alfred North, and Bertrand Russell. Principia Mathematica, 3 vols, Cambridge University Press, 1910, 1912, and 1913. Second edition, 1925 (Vol. 1), 1927 (Vols 2, 3).
External links
- [https://archive.org/stream/PrincipiaMathematicaVolumeI/WhiteheadRussell-PrincipiaMathematicaVolumeI#page/n709/mode/2up List of notation in Principia Mathematica at the end of volume I]
- The Notation in Principia Mathematica—by Bernard Linsky.
- Principia Mathematica online (University of Michigan Historical Math Collection):
- Volume I
- Volume II
- Volume III
- Proposition ✸54.43 in a more modern notation (Metamath)
11 : Large-scale mathematical formalization projects|Analytic philosophy literature|Mathematical logic|Mathematics books|Logic books|Mathematics literature|Books by Bertrand Russell|Works by Alfred North Whitehead|Mathematical notation|Logic symbols|Glossaries of mathematics
- Rogers Gaines
- Roger S. Goody
- Roger Shallot
- Rogers, Harold
- Roger Sharpley
- Rogers/Hart
- Roger Shattuck Prize for Criticism
- Roger Sheck
- Rogers, Henry
- Roger Sherman Baldwin Foster
- Roger Sherman (disambiguation)
- Roger Sherman (filmmaker)
- Roger Sherman (Maine politician)
- Roger Sherman (politician)
- Rogers High School (Newport, Rhode Island)
- Roger Shillingford
- Rogers Historic District
- Rogers Hometown Hockey
- Rogers House (Morgantown, West Virginia)
- Roger Shuler
- Roger Shuy
- Rogers' Hybrid Nr. 15
- Roger Simon (disambiguation)
- Roger Simon (journalist)
- Rogersiomyces