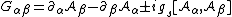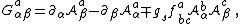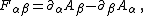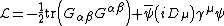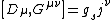- Definition Tensor components Differential forms Comparison with the electromagnetic tensor
- QCD Lagrangian density
- Gauge transformations
- Equations of motion
- See also
- References Notes Further reading Books Selected papers
- External links
In theoretical particle physics, the gluon field strength tensor is a second order tensor field characterizing the gluon interaction between quarks.
The strong interaction is one of the fundamental interactions of nature, and the quantum field theory (QFT) to describe it is called quantum chromodynamics (QCD). Quarks interact with each other by the strong force due to their color charge, mediated by gluons. Gluons themselves possess color charge and can mutually interact.
The gluon field strength tensor is a rank 2 tensor field on the spacetime with values in the adjoint bundle of the chromodynamical SU(3) gauge group (see vector bundle for necessary definitions). Throughout, Latin indices (typically {{math|a, b, c, n}}) take values 1, 2, ..., 8 for the eight gluon color charges, while Greek indices (typically {{math|α, β, μ, ν}}) take values 0 for timelike components and 1, 2, 3 for spacelike components of four-vectors and four-dimensional spacetime tensors. Throughout all equations, the summation convention is used on all color and tensor indices, unless explicitly stated there is no sum to be taken.
Definition
Below the definitions (and most of the notation) follow K. Yagi, T. Hatsuda, Y. Miake[1] and Greiner, Schäfer.[2]
Tensor components
The tensor is denoted {{math|G}}, (or {{math|F}}, {{math|{{overline|F}}}}, or some variant), and has components defined proportional to the commutator of the quark covariant derivative {{math|Dμ}}:[2][3]
where:
in which
- {{math|i}} is the imaginary unit;
- {{math|gs}} is the coupling constant of the strong force;
- {{math|ta {{=}} λa/2}} are the Gell-Mann matrices {{math|λa}} divided by 2;
- {{math|a}} is a color index in the adjoint representation of SU(3) which take values 1, 2, ..., 8 for the eight generators of the group, namely the Gell-Mann matrices;
- {{math|μ}} is a spacetime index, 0 for timelike components and 1, 2, 3 for spacelike components;
 expresses the gluon field, a spin-1 gauge field or, in differential-geometric parlance, a connection in the SU(3) principal bundle;
expresses the gluon field, a spin-1 gauge field or, in differential-geometric parlance, a connection in the SU(3) principal bundle;-
 are its four (coordinate-system dependent) components, that in a fixed gauge are {{gaps|3|×|3}} traceless Hermitian matrix-valued functions, while
are its four (coordinate-system dependent) components, that in a fixed gauge are {{gaps|3|×|3}} traceless Hermitian matrix-valued functions, while 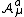 are 32 real-valued functions, the four components for each of the eight four-vector fields.
are 32 real-valued functions, the four components for each of the eight four-vector fields.
Different authors choose different signs.
Expanding the commutator gives;
Substituting  and using the commutation relation
and using the commutation relation  for the Gell-Mann matrices (with a relabeling of indices), in which {{math|f abc}} are the structure constants of SU(3), each of the gluon field strength components can be expressed as a linear combination of the Gell-Mann matrices as follows:
for the Gell-Mann matrices (with a relabeling of indices), in which {{math|f abc}} are the structure constants of SU(3), each of the gluon field strength components can be expressed as a linear combination of the Gell-Mann matrices as follows:
so that:[4][5]
where again {{math|a, b, c {{=}} 1, 2, ..., 8}} are color indices. As with the gluon field, in a specific coordinate system and fixed gauge {{math|Gαβ}} are {{gaps|3|×|3}} traceless Hermitian matrix-valued functions, while {{math|Gaαβ}} are real-valued functions, the components of eight four-dimensional second order tensor fields.
Differential forms
The gluon color field can be described using the language of differential forms, specifically as an adjoint bundle-valued curvature 2-form (note that fibers of the adjoint bundle are the su(3) Lie algebra);
where 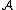 is the gluon field, a vector potential 1-form corresponding to {{math|G}} and {{math|∧}} is the (antisymmetric) wedge product of this algebra, producing the structure constants {{math|f abc}}. The Cartan-derivative of the field form (i.e. essentially the divergence of the field) would be zero in the absence of the "gluon terms", i.e. those
is the gluon field, a vector potential 1-form corresponding to {{math|G}} and {{math|∧}} is the (antisymmetric) wedge product of this algebra, producing the structure constants {{math|f abc}}. The Cartan-derivative of the field form (i.e. essentially the divergence of the field) would be zero in the absence of the "gluon terms", i.e. those 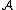 which represent the non-abelian character of the SU(3).
which represent the non-abelian character of the SU(3).
A more mathematically formal derivation of these same ideas (but a slightly altered setting) can be found in the article on metric connections.
Comparison with the electromagnetic tensor
This almost parallels the electromagnetic field tensor (also denoted {{math|F }}) in quantum electrodynamics, given by the electromagnetic four-potential {{math|A}} describing a spin-1 photon;
or in the language of differential forms:
The key difference between quantum electrodynamics and quantum chromodynamics is that the gluon field strength has extra terms which lead to self-interactions between the gluons and asymptotic freedom. This is a complication of the strong force making it inherently non-linear, contrary to the linear theory of the electromagnetic force. QCD is a non-abelian gauge theory. The word non-abelian in group-theoretical language means that the group operation is not commutative, making the corresponding Lie algebra non-trivial.
QCD Lagrangian density
{{see also|Classical field theory}}Characteristic of field theories, the dynamics of the field strength are summarized by a suitable Lagrangian density and substitution into the Euler–Lagrange equation (for fields) obtains the equation of motion for the field. The Lagrangian density for massless quarks, bound by gluons, is:[2]
where "tr" denotes trace of the {{gaps|3|×|3}} matrix {{math|GαβGαβ}}, and {{math|γμ}} are the {{gaps|4|×|4}} gamma matrices. In the fermionic term  , both color and spinor indices are suppressed. With indices explicit,
, both color and spinor indices are suppressed. With indices explicit,  where
where  are color indices and
are color indices and  are Dirac spinor indices.
are Dirac spinor indices.
Gauge transformations
{{main|Gauge theory}}In contrast to QED, the gluon field strength tensor is not gauge invariant by itself. Only the product of two contracted over all indices is gauge invariant.
Equations of motion
Treated as a classical field theory, the equations of motion for the[1] quark fields are:
which is like the Dirac equation, and the equations of motion for the gluon (gauge) fields are:
which are similar to the Maxwell equations (when written in tensor notation). More specifically, these are the Yang–Mills equations for quark and gluon fields. The color charge four-current is the source of the gluon field strength tensor, analogous to the electromagnetic four-current as the source of the electromagnetic tensor. It is given by
which is a conserved current since color charge is conserved. In other words, the color four-current must satisfy the continuity equation:
See also
- Quark confinement
- Gell-Mann matrices
- Field (physics)
- Yang–Mills field
- Eightfold Way (physics)
- Einstein tensor
- Wilson loop
- Wess–Zumino gauge
- Quantum chromodynamics binding energy
References
Notes
2. ^1 2 {{cite book|title=Quantum Chromodynamics|author1=W. Greiner |author2=G. Schäfer |year=1994|chapter=4|publisher=Springer|chapter-url=https://books.google.com/books/about/Quantum_Chromodynamics.html?id=gzYHNhp9KTIC|isbn=978-3-540-57103-2}}
3. ^{{cite journal|title=Highly improved lattice field-strength tensor|author1=S.O. Bilson-Thompson |author2=D.B. Leinweber |author3=A.G. Williams |year=2003|journal=Annals of Physics|volume=304 |issue=1|pages=1–21|arxiv =hep-lat/0203008 |url=http://www.sciencedirect.com/science/article/pii/S0003491603000095 |doi=10.1016/s0003-4916(03)00009-5|bibcode=2003AnPhy.304....1B}}
4. ^{{cite news|title=The field strength correlator from QCD sum rules|author1=M. Eidemüller |author2=H.G. Dosch |author3=M. Jamin |orig-year=1999|year=2000|publisher=|location=Heidelberg, Germany|journal=Nucl. Phys. B Proc. Suppl. |volume=86 |pages=421–425 |arxiv=hep-ph/9908318|bibcode=2000NuPhS..86..421E|doi=10.1016/S0920-5632(00)00598-3}}
5. ^{{cite book|title = Advanced Topics in Quantum Field Theory: A Lecture Course |edition = |author= M. Shifman|publisher = Cambridge University Press|year=2012 |isbn = 978-0521190848|url= https://books.google.com/books?id=zeQuWycXV3oC&pg=PA473&dq=gluon+field+strength+tensor#v=onepage&q=gluon%20field%20strength%20tensor&f=false}}
Further reading
Books
- {{cite book|title = Quarks: the stuff of matter|edition = |author = H. Fritzsch| series = |publisher = Allen lane|year=1982|isbn = 978-0-7139-15334}}
- {{cite book|title = Particle Physics |edition = 3rd |author1=B.R. Martin |author2=G. Shaw | series = Manchester Physics Series|publisher = John Wiley & Sons|year=2009|isbn = 978-0-470-03294-7}}
- {{cite book|title = The Physics of the Quark-Gluon Plasma: Introductory Lectures|edition = |author1=S. Sarkar |author2=H. Satz |author3=B. Sinha |publisher = Springer|year=2009|isbn = 978-3642022852|url=https://books.google.com/books?id=1WPV0NSenZ4C&pg=PA344&dq=gluon+field+strength+tensor#v=onepage&q=gluon%20field%20strength%20tensor&f=false}}
- {{cite book|title = Hadrons, Quarks and Gluons: Proceedings of the Hadronic Session of the Twenty-Second Rencontre de Moriond, Les Arcs-Savoie-France|edition = |author= J. Thanh Van Tran (editor)|publisher = Atlantica Séguier Frontières|year=1987|isbn = 978-2863320488|url=https://books.google.com/books?id=Vo48UfeBaG4C&pg=PA615&dq=gluon+field+strength+tensor#v=onepage&q=gluon%20field%20strength%20tensor&f=false}}
- {{cite book|title = Chiral Quark Dynamics|edition = |author1=R. Alkofer |author2=H. Reinhart |publisher = Springer|year=1995 |isbn = 978-3540601371|url=https://books.google.com/books?id=fDENwIMAc50C&pg=PA7&dq=gluon+field+strength+tensor#v=onepage&q=gluon%20field%20strength%20tensor&f=false}}
- {{cite book|title = Hadronic Production of ψ(2S) Cross Section and Polarization|edition = |author= K. Chung|publisher = ProQuest|year=2008 |isbn = 978-0549597742|url=https://books.google.com/books?id=ETrMNvqLrXUC&pg=PA2&dq=gluon+field+strength+tensor#v=onepage&q=gluon%20field%20strength%20tensor&f=false}}
- {{cite book|title = Foundations of Perturbative QCD|edition = |author= J. Collins|publisher = Cambridge University Press|year=2011 |isbn = 978-0521855334|url= https://books.google.com/books?id=0xGi1KW9vykC&pg=PA233&dq=gluon+field+strength+tensor#v=onepage&q=gluon%20field%20strength%20tensor&f=false}}
- {{cite book|title = Standard Model of Particle Physics|edition = |author1=W.N.A. Cottingham |author2=D.A.A. Greenwood |publisher = Cambridge University Press|year=1998 |isbn = 978-0521588324|url= https://books.google.com/books?id=XSseBp7y19MC&pg=PR16&dq=gluon+field+strength+tensor#v=onepage&q=gluon%20field%20strength%20tensor&f=false}}
Selected papers
- {{cite journal
|title=QCD evolutions of twist-3 chirality-odd operators
|author1=J.P. Maa |author2=Q. Wang |author3=G.P. Zhang |year=2012
|journal=Physics Letters B
|doi=10.1016/j.physletb.2012.12.007
|arxiv = 1210.1006 |bibcode = 2013PhLB..718.1358M |volume=718 |issue=4–5 |pages=1358–1363}}
- {{cite journal
|title=Field strength correlators in full QCD
|author=M. D’Elia, A. Di Giacomo, E. Meggiolaro
|year=1997
|journal=Physics Letters B
|arxiv=hep-lat/9705032
|bibcode = 1997PhLB..408..315D |doi = 10.1016/S0370-2693(97)00814-9
|volume=408
|issue=1–4
|pages=315–319}}
- {{cite arXiv
|title=Gauge Invariant Field Strength Correlators In QCD
|author1=A. Di Giacomo |author2=M. D’elia |author3=H. Panagopoulos |author4=E. Meggiolaro |year=1998
|eprint = hep-lat/9808056
}}
- {{cite journal
|title=A Virial Theorem for the Kinetic Energy of a Heavy Quark inside Hadrons
|author=M. Neubert
|year=1993
|journal=Physics Letters B
|arxiv=hep-ph/9311232
|bibcode = 1994PhLB..322..419N |doi = 10.1016/0370-2693(94)91174-6
|volume=322
|issue=4
|pages=419–424}}
- {{cite journal
|title=Field strength correlators and dual effective dynamics in QCD
|author1=M. Neubert |author2=N. Brambilla |author3=H.G. Dosch |author4=A. Vairo |year=1998
|journal=Physical Review D
|arxiv = hep-ph/9311232
|doi=10.1103/PhysRevD.58.034010
|bibcode = 1998PhRvD..58c4010B |volume=58|issue=3 |pages=034010 }}
- {{cite news
|title=QCD sum-rule calculation of the kinetic energy and chromo-interaction of heavy quarks inside mesons
|author=M. Neubert
|year=1996
|journal=Physics Letters B
|url=ftp://79.110.128.93/books/physics,%20math/%D0%96%D1%83%D1%80%D0%BD%D0%B0%D0%BB%D1%8B/Phys%20Letters%20B/Volume%20389,%20Issue%204,%20pp.%20631-830%20(26%20December%201996)/Matthias%20Neubert%20-%20QCD%20sum-rule%20calculation%20of%20the%20kinetic%20energy%20and%20chromo-interaction%20of%20heavy%20quarks%20inside%20mesons.pdf
}}
External links
- {{cite news|title=QCD |author=K. Ellis |year=2005 |publisher=Fermilab |journal= |url=http://theory.fnal.gov/people/ellis/Talks/FNAL/l1_s.pdf |deadurl=unfit |archiveurl=https://web.archive.org/web/20060926033047/http://theory.fnal.gov/people/ellis/Talks/FNAL/l1_s.pdf |archivedate=September 26, 2006 }}
- {{cite web|accessdate=2013-10-17
|title=Chapter 2: The QCD Lagrangian
|location=Technische Universität München
|url=http://www.t39.ph.tum.de/T39_files/Lectures_files/StrongInteraction2011/QCDkap2.pdf}}{{tensors}}
- Guruswami–Sudan list decoding algorithm
- Gurutag
- Guru Teg Bahadur ji
- Guru Teg Bahadur Khalsa Senior Secondary School, Malout
- Guru Tegh Bahadur Nagar railway station
- Gurutzeta/Cruces (Metro Bilbao station)
- Gurutzeta/Cruces Station
- Gurutzeta KFT
- Guru Vandana (song)
- Guruvayoor (Assembly constituency)
- Guruvayoor Kesavan
- Guruvayoor Keshavan
- Guruvayoor Sivaji
- Guruvayur - Chennai Egmore Express
- Guruvayur-Chennai Egmore Express
- Guruvayur Kesavan (film)
- Guruvayur Railway Station
- Guruvayur railway station
- Guruwar Peth
- Guruwar Peth, Pune
- Guruwar Peth,Pune
- GURUŠ (young man Sumerogram)
- Gurvan
- Gurvand, Duke of Brittany
- Gurvan (disambiguation)