勾股数Gougushu

在西方称为毕达哥拉斯数，即不定方程
x²+y²＝z² (1)
的正整数解， 几何意义为边长均是正整数的直角三角形。在古代， 有时也取正有理数解。
初等数论中有如下定理：不定方程(1)的适合x>0, y>0, z>0, (x, y) =1, 2|x的解， 必可表示为
x=2ab, y=a²-b², z=a²+b²
(a, b) =1, a>b>0, a、b一奇一偶的形
式， 且如此的 (x, y, z)与自然数对 (a, b) 一一对应。
寻求边长均为正整数或正有理数的直角三角形，这一问题在数学发展的早期曾先后引起过巴比伦、希腊、印度、中国， 可能还有埃及等各古代民族的注意。埃及人给出了最简单的一组勾股数(3,4,5)。在成书于公元前8——前5世纪的印度的《祭坛建筑》中不仅记载了勾股定理，而且记载了6组勾股数：3,4, 5:5.12, 13; 7. 24, 25; 8, 15, 17; 12, 35, 37; 15, 36,39。说明他们在那时已经有了求勾股数的某种方法。实际上， 这6组勾股数均可归入两个互补的模式
x: y: z=2a: (a²-1): (a²+1) (2)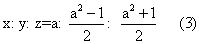
在公元前5——前4世纪， 希腊的毕达哥拉斯学派和柏拉图学派也给出了这两个公式。
在一块属于公元前1900——前1600年间的古巴比伦泥板上，记载着令人惊叹的数学内容。它曾是普林顿(Plimpton,G. A.)的个人收藏品，现存美国哥伦比亚大学图书馆，编号为322，因而被称为“普林顿322号泥板” （如图）。

普林顿322号泥板
泥板的左半部分已经遗失，右半部分用巴比伦的 60 进位值制刻着 4 列、15 行数字。若按
从左至右的顺序把这4列数字分别标为A、B、C、D，则D为行的序号，从1直到15;B、C的意义为：若把勾股数公式写为

x=2ab, y=a²-b², z=a²+b²

则B、C列中的数分别对应于y、z;A列则对应于
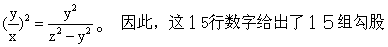
数。如果把A列用相应的x值代替，并给出与(x,y,z)相应的参数组(a,b)，就可以列出下表（用今天的数码）:

x	y	z	a	b	序号
120 3 456 4 800 13 500 72 360 2 700	119 3 367 4 601 12 709 65 319 2 291	169 4 825 6 649 18 541 97 481 3 541	12 64 75 125 9 20 54	5 27 32 54 4 9 25	1 2 3 4 5 6 7

x	y	z	a	b	序号
960 600 6 480 60	799 481 4 961 45	1 249 769 8 161 75	32 25 81	15 12 40	8 9 10 11
2 400 2 40 2 700 90	1 679 161 1 771 56	2 929 289 3 229 106	48 15 50 9	25 8 37 5	12 13 14 15

第11行在60进位值制中的意义实际应为
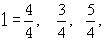
相应于勾股数(3,4,5)，参数组为(2.1)。这15组勾股数，既不可能是通过试验的方法得到的，也无法归入任何特殊的模式，因此，它说明当时巴比伦人很可能已经掌握了推求勾股数的一般公式。
在希腊，欧几里得在《几何原本》中给出了今天的勾股数公式的等价形式，并严格地证明了它。在中国，《九章算术》勾股章中给出了与今天的公式完全一致的形式， 严格的证明是在公元3世纪由刘徽明确地给出的。
公元3世纪，丢番图在他的《算术》中重新叙述了欧几里得已研究过的勾股数问题：“把 一给定的平方数分解为两个平方数”。由于他研究的是正有理数解而不限于整数， 上述问题实际上与一般勾股数问题是完全一致的。大约在1636年，这个问题被法国大数学家费尔马进一步研究， 提出
xⁿ+yⁿ＝zⁿ n>2
没有正整数解，即著名的费尔马大定理（参见该条），对后世数学的发展产生了深远的影响。