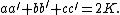“Harcourt's theorem”的意思、由来-开放百科全书

词条

Harcourt's theorem

释义

Statement
Degenerate case
Extension
Dual property
References

Harcourt's theorem is a formula in geometry for the area of a triangle, as a function of its side lengths and the perpendicular distances of its vertices from an arbitrary line tangent to its incircle.^[1]

The theorem is named after J. Harcourt, an Irish professor.^[2]

Statement

Let a triangle be given with vertices A, B, and C, opposite sides of lengths a, b, and c, area K, and a line that is tangent to the triangle's incircle at any point on that circle. Denote the signed perpendicular distances of the vertices from the line as a ', b ', and c ', with a distance being negative if and only if the vertex is on the opposite side of the line from the incenter. Then

Degenerate case

If the tangent line contains one of the sides of the triangle, then two of the distances are zero and the formula collapses to the familiar formula that twice the area of a triangle is a base (the coinciding triangle side) times the altitude from that base.

Extension

If the line is instead tangent to the excircle opposite, say, vertex A of the triangle, then^[1]{{rp|Thm.3}}

Dual property

If rather than a', b', c' referring to distances from a vertex to an arbitrary incircle tangent line, they refer instead to distances from a sideline to an arbitrary point, then the equation

remains true.^[3]{{rp|p. 11}}

References

1. ^¹{{citation | last1 = Dergiades | first1 = Nikolaos | last2 = Salazar | first2 = Juan Carlos | journal = Forum Geometricorum | mr = 2004117 | pages = 117–124 | title = Harcourt's theorem | url = http://forumgeom.fau.edu/FG2003volume3/FG200313.pdf | volume = 3 | year = 2003}}.
2. ^{{citation|title=Exercises de géométrie: comprenant l'exposé des méthodes géométriques et 2000 questions résolues|series=Cours de mathématiques elementaires|first=F.|last=G.-M.|edition=5th|publisher=Maison A. Mame et fils (Tours) & J. de Gigord (Paris)|year=1912|page=750|url=http://quod.lib.umich.edu/u/umhistmath/ACV3924.0001.001/780|contribution=Théorème de Harcourt|language=French}}.
3. ^Whitworth, William Allen. Trilinear Coordinates and Other Methods of Modern Analytical Geometry of Two Dimensions, Forgotten Books, 2012 (orig. Deighton, Bell, and Co., 1866). http://www.forgottenbooks.com/search?q=Trilinear+coordinates&t=books

3 : Circles|Triangle geometry|Theorems in geometry

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。