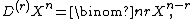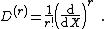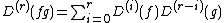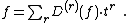“Hasse derivative”的意思、由来-开放百科全书

词条

Hasse derivative

释义

Definition
Properties
References

In mathematics, the Hasse derivative is a generalisation of the derivative which allows the formulation of Taylor's theorem in coordinate rings of algebraic varieties.

Definition

Let k[X] be a polynomial ring over a field k. The r-th Hasse derivative of Xⁿ is

if n ≥ r and zero otherwise.^[1] In characteristic zero we have

Properties

The Hasse derivative is a generalized derivation on k[X] and extends to a generalized derivation on the function field k(X),^[1] satisfying an analogue of the product rule

and an analogue of the chain rule.^[2] Note that the 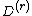are not themselves derivations in general, but are closely related.

A form of Taylor's theorem holds for a function f defined in terms of a local parameter t on an algebraic variety:^[3]

References

1. ^¹Goldschmidt (2003) p.28
2. ^Goldschmidt (2003) p.29
3. ^Goldschmidt (2003) p.64

{{cite book | last=Goldschmidt | first=David M. | title=Algebraic functions and projective curves | series=Graduate Texts in Mathematics | volume=215 | location=New York, NY | publisher=Springer-Verlag | year=2003 | isbn=0-387-95432-5 | zbl=1034.14011 }}

1 : Differential algebra

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。