“Hautus lemma”的意思、由来-开放百科全书

词条

Hautus lemma

释义

The main result
Hautus Lemma for controllability Hautus Lemma for stabilizability Hautus Lemma for observability Hautus Lemma for detectability
References

In control theory and in particular when studying the properties of a linear time-invariant system in state space form, the Hautus lemma, named after Malo Hautus, can prove to be a powerful tool. This result appeared first in ^[1] and.^[2] Today it can be found in most textbooks on control theory.

The main result

There exist multiple forms of the lemma.

Hautus Lemma for controllability

The Hautus lemma for controllability says that given a square matrix and a 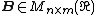the following are equivalent:

The pair is controllable
For all it holds that
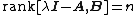
For all that are eigenvalues of it holds that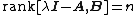

Hautus Lemma for stabilizability

The Hautus lemma for stabilizability says that given a square matrix and a 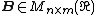the following are equivalent:

The pair is stabilizable
For all that are eigenvalues of and for which 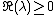it holds that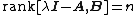

Hautus Lemma for observability

The Hautus lemma for observability says that given a square matrix and a 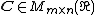the following are equivalent:

The pair 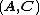is observable
For all it holds that
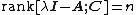
For all that are eigenvalues of it holds that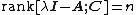

Hautus Lemma for detectability

The Hautus lemma for detectability says that given a square matrix and a 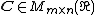the following are equivalent:

The pair 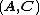is detectable
For all that are eigenvalues of and for which 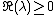it holds that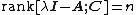

References

{{cite book|last=Sontag|first=Eduard D.|title=Mathematical Control Theory: Deterministic Finite-Dimensional Systems.|year=1998|publisher=Springer|location=New York|isbn=0-387-98489-5}}
{{cite book|last=Zabczyk|first=Jerzy|title=Mathematical Control Theory – An introduction|year=1995|publisher=Birkhauser|location=Boston|isbn=3-7643-3645-5}}

1. ^{{cite book|last=Belevitch|first=V.|title=Classical Network Theory|year=1968|publisher=Holden–Day|location=San Francisco}}
2. ^{{cite book|last=Popov|first=V. M.|title=Hyperstability of Control Systems|year=1973|publisher=Springer-Verlag|location=Berlin|pages=320}}

2 : Control theory|Lemmas

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。