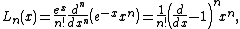“Rodrigues' formula”的意思、由来-开放百科全书

词条

Rodrigues' formula

释义

Statement
References

{{for|the 3-dimensional rotation formula|Rodrigues' rotation formula}}

In mathematics, Rodrigues' formula (formerly called the Ivory–Jacobi formula) is a formula for the Legendre polynomials independently introduced by {{harvs|txt|authorlink=Olinde Rodrigues|first=Olinde|last=Rodrigues|year=1816}}, {{harvs|txt|authorlink=James Ivory (mathematician)|first=Sir James|last= Ivory|year=1824}} and {{harvs|txt|authorlink=Carl Gustav Jacob Jacobi|first=Carl Gustav|last=Jacobi|year=1827}}. The name "Rodrigues formula" was introduced by Heine in 1878, after Hermite pointed out in 1865 that Rodrigues was the first to discover it. The term is also used to describe similar formulas for other orthogonal polynomials. {{harvtxt|Askey|2005}} describes the history of the Rodrigues formula in detail.

Statement

Let 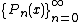be a sequence of orthogonal polynomials satisfying the orthogonality condition

where, is a suitable weight function, are constants and is the Kronecker delta. If the weight function satisfies the following differential equation (called Pearson's differential equation),

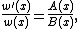
where is a polynomial with degree at most 1 and 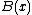is a polynomial with degree at most 2 and, further, the limits

then, it can be shown that satisfies a recurrence relation of the form,

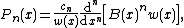
for a given constants . This relation is called Rodrigues' type formula, or just Rodrigues' formula.^[1]

The most known applications of Rodrigues' type formulas are the formulas for Legendre, Laguerre and Hermite polynomials:

Rodrigues stated his formula for Legendre polynomials :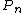

Laguerre polynomials are usually denoted L₀, L₁, ..., and the Rodrigues formula can be written as

The Rodrigues formula for the Hermite polynomial can be written as

.

Similar formulae hold for many other sequences of orthogonal functions arising from Sturm-Liouville equations, and these are also called the Rodrigues formula (or Rodrigues' type formula) for that case, especially when the resulting sequence is polynomial.

References

1. ^{{Cite web|url=https://www.encyclopediaofmath.org/index.php/Rodrigues_formula|title=Rodrigues formula - Encyclopedia of Mathematics|website=www.encyclopediaofmath.org|language=en|access-date=2018-04-18}}

{{Citation | last1=Askey | first1=Richard |authorlink=Richard Askey| editor1-last=Altmann | editor1-first=Simón L. | editor2-last=Ortiz | editor2-first=Eduardo L. | title=Mathematics and social utopias in France: Olinde Rodrigues and his times | url=https://books.google.com/books?id=oTyJYUx8Jr4C&pg=PA105 | publisher=American Mathematical Society | location=Providence, R.I. | series= History of mathematics | isbn=978-0-8218-3860-0 | year=2005 | volume=28 | chapter=The 1839 paper on permutations: its relation to the Rodrigues formula and further developments | pages=105–118}}
{{citation

| title = On the Figure Requisite to Maintain the Equilibrium of a Homogeneous Fluid Mass That Revolves Upon an Axis
| last=Ivory|first= James
| journal = Philosophical Transactions of the Royal Society of London
| volume = 114
|year=1824
| pages = 85–150
| jstor = 107707
| publisher = The Royal Society
| doi=10.1098/rstl.1824.0008
}}

{{Citation | last1=Jacobi | first1=C. G. J. | title=Ueber eine besondere Gattung algebraischer Functionen, die aus der Entwicklung der Function (1 − 2xz + z²)^1/2 entstehen. | language=German | doi=10.1515/crll.1827.2.223 | year=1827 | journal=Journal für die Reine und Angewandte Mathematik | issn=0075-4102 | volume=2 | pages=223–226}}
{{MacTutor|id=Rodrigues|title=Olinde Rodrigues}}
{{citation|first=Olinde|last= Rodrigues|authorlink=Olinde Rodrigues|series=(Thesis for the Faculty of Science of the University of Paris)|title=De l'attraction des sphéroïdes|journal=Correspondence sur l'École Impériale Polytechnique|volume=3|issue=3|year=1816|pages= 361–385|url = https://books.google.com/books?id=dp4AAAAAYAAJ&hl=en&pg=PA361#v=onepage&q&f=false}}

1 : Orthogonal polynomials

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。