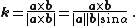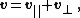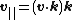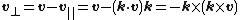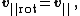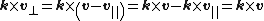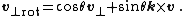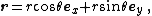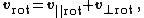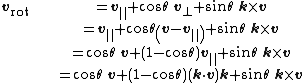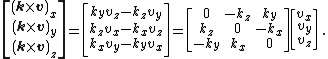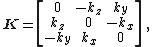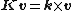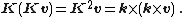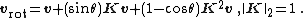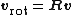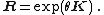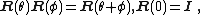- Statement
- Derivation
- Matrix notation
- See also
- References
- External links
This article is about the Rodrigues' rotation formula, which is distinct from the related Euler–Rodrigues parameters and The Euler–Rodrigues formula for 3D rotation.
In the theory of three-dimensional rotation, Rodrigues' rotation formula, named after Olinde Rodrigues, is an efficient algorithm for rotating a vector in space, given an axis and angle of rotation. By extension, this can be used to transform all three basis vectors to compute a rotation matrix in {{math|SO(3)}}, the group of all rotation matrices, from an axis–angle representation. In other words, the Rodrigues' formula provides an algorithm to compute the exponential map from {{math|so(3)}}, the Lie algebra of {{math|SO(3)}}, to {{math|SO(3)}} without actually computing the full matrix exponential.
Statement
If {{math|v}} is a vector in {{math|ℝ3}} and {{math|k}} is a unit vector describing an axis of rotation about which {{math|v}} rotates by an angle {{mvar|θ}} according to the right hand rule, the Rodrigues formula for the rotated vector {{math|vrot}} is
{{Equation box 1|indent =:
|equation =
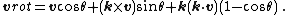
|cellpadding= 6
|border
|border colour = #0073CF
|bgcolor=#F9FFF7}}
An alternative statement is to write the axis vector as a cross product {{math|a × b}} of any two nonzero vectors {{math|a}} and {{math|b}} which define the plane of rotation, and the sense of the angle {{math|θ}} is measured away from {{math|a}} and towards {{math|b}}. Letting {{math|α}} denote the angle between these vectors, the two angles {{math|θ}} and {{math|α}} are not necessarily equal, but they are measured in the same sense. Then the unit axis vector can be written
This form may be more useful when two vectors defining a plane are involved. An example in physics is the Thomas precession which includes the rotation given by Rodrigues' formula, in terms of two non-collinear boost velocities, and the axis of rotation is perpendicular to their plane.
Derivation
Let {{math|k}} be a unit vector defining a rotation axis, and let {{math|v}} be any vector to rotate about {{math|k}} by angle {{math|θ}} (right hand rule, anticlockwise in the figure).
Using the dot and cross products, the vector {{math|v}} can be decomposed into components parallel and perpendicular to the axis {{math|k}},
where the component parallel to {{math|k}} is
called the vector projection of {{math|v}} on {{math|k}}, and the component perpendicular to {{math|k}} is
called the vector rejection of {{math|v}} from {{math|k}}.
The vector {{math|k × v}} can be viewed as a copy of {{math|v⊥}} rotated anticlockwise by 90° about {{math|k}}, so their magnitudes are equal but directions are perpendicular. Likewise the vector {{math|k × (k × v)}} a copy of {{math|v⊥}} rotated anticlockwise through {{math|180°}} about {{math|k}}, so that {{math|k × (k × v)}} and {{math|v⊥}} are equal in magnitude but in opposite directions (i.e. they are negatives of each other, hence the minus sign). Expanding the vector triple product establishes the connection between the parallel and perpendicular components, for reference the formula is {{math|a × (b × c) {{=}} (a · c)b − (a · b)c}} given any three vectors {{math|a}}, {{math|b}}, {{math|c}}.
The component parallel to the axis will not change magnitude nor direction under the rotation,
only the perpendicular component will change direction but retain its magnitude, according to
and since {{math|k}} and {{math|v∥}} are parallel, their cross product is zero {{math|k × v∥ {{=}} 0}}, so that
and it follows
This rotation is correct since the vectors {{math|v⊥}} and {{math|k × v}} have the same length, and {{math|k × v}} is {{math|v⊥}} rotated anticlockwise through {{math|90°}} about {{math|k}}. An appropriate scaling of {{math|v⊥}} and {{math|k × v}} using the trigonometric functions sine and cosine gives the rotated perpendicular component. The form of the rotated component is similar to the radial vector in 2D planar polar coordinates {{math|(r, θ)}} in the Cartesian basis
where {{math|ex}}, {{math|ey}} are unit vectors in their indicated directions.
Now the full rotated vector is
By substituting the definitions of {{math|v∥rot}} and {{math|v⊥rot}} in the equation results in
Matrix notation
Representing {{math|v}} and {{math|k × v}} as column matrices, the cross product can be expressed as a matrix product
Letting {{math|K}} denote the "cross-product matrix" for the unit vector {{math|k}},
the matrix equation is, symbolically,
for any vector {{math|v}}. (In fact, {{math|K}} is the unique matrix with this property. It has eigenvalues 0 and {{math|±i}}).
Iterating the cross product on the right is equivalent to multiplying by the cross product matrix on the left, in particular
Moreover, since {{math|k}} is a unit vector, {{math|K}} has unit 2-norm. The previous rotation formula in matrix language is therefore
Note the coefficient of the leading term is now 1, in this notation: see the Lie-Group discussion below.
Factorizing the {{math|v}} allows the compact expression
where
{{Equation box 1|indent =:
|equation =
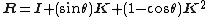
|cellpadding= 6
|border
|border colour = #0073CF
|bgcolor=#F9FFF7}}
is the rotation matrix through an angle {{mvar|θ}} counterclockwise about the axis {{math|k}}, and {{math|I}} the {{nowrap|3 × 3}} identity matrix. This matrix {{math|R}} is an element of the rotation group {{math|SO(3)}} of {{math|ℝ3}}, and {{math|K}} is an element of the Lie algebra {{math|so(3)}} generating that Lie group (note that {{math|K}} is skew-symmetric, which characterizes {{math|so(3)}}).
In terms of the matrix exponential,
To see that the last identity holds, one notes that
characteristic of a one-parameter subgroup, i.e. exponential, and that the formulas match for infinitesimal {{mvar|θ}}.
For an alternative derivation based on this exponential relationship, see exponential map from {{math|so(3)}} to {{math|SO(3)}}. For the inverse mapping, see log map from {{math|SO(3)}} to {{math|so(3)}}.
See also
- Axis angle
- Rotation (mathematics)
- SO(3) and SO(4)
- Euler–Rodrigues formula
References
- Leonhard Euler, "Problema algebraicum ob affectiones prorsus singulares memorabile", Commentatio 407 Indicis Enestoemiani, Novi Comm. Acad. Sci. Petropolitanae 15 (1770), 75–106.
- Olinde Rodrigues, "Des lois géometriques qui regissent les déplacements d' un systéme solide dans l' espace, et de la variation des coordonnées provenant de ces déplacement considérées indépendant des causes qui peuvent les produire", J. Math. Pures Appl. 5 (1840), 380–440.
- Don Koks, (2006) Explorations in Mathematical Physics, Springer Science+Business Media,LLC. {{isbn|0-387-30943-8}}. Ch.4, pps 147 et seq. A Roundabout Route to Geometric Algebra'
External links
- {{MathWorld |title=Rodrigues' Rotation Formula |urlname=RodriguesRotationFormula}}
- Johan E. Mebius, [https://arxiv.org/abs/math/0701759 Derivation of the Euler-Rodrigues formula for three-dimensional rotations from the general formula for four-dimensional rotations.], arXiv General Mathematics 2007.
- For another descriptive example see http://chrishecker.com/Rigid_Body_Dynamics#Physics_Articles, Chris Hecker, physics section, part 4. "The Third Dimension" – on page 3, section ``Axis and Angle, http://chrishecker.com/images/b/bb/Gdmphys4.pdf
- Death of Phoebe Prince
- Death of Pope Pius XII
- Death Of Princess Diana
- Death of Princess Diana Conspiracy Theories
- Death of Princess Diana conspiracy theories
- Death of Pyotr Il'yich Tchaikovsky
- Death of Raja Ahmed
- Death of Ramin Pourandarjani
- Death of Robert Dziekanski
- Death of Robert Dziekański
- Death of Robert Hill
- Death of Roger Sylvester
- Death of Roland Ratzenberger
- Death of Ryan Halligan
- Death Of Samantha
- Death of Sardanapolus
- Death of Sebastien Briat
- Death of Seyed Ali Mousavi
- Death of Sophie Toscan du Plantier
- Death of Stephany Flores
- Death of Stephany Tatiana Flores Ramírez
- Death of Stephen Gately
- Death of Steve Irwin
- Death of Stevie Ray Vaughan
- Death of Superboy