- Network Architecture
- Training
- References
In machine learning, a Hyper basis function network, or HyperBF network, is a generalization of radial basis function (RBF) networks concept, where the Mahalanobis-like distance is used instead of Euclidean distance measure. Hyper basis function networks were first introduced by Poggio and Girosi in the 1990 paper “Networks for Approximation and Learning”.[1][2]
Network Architecture
The typical HyperBF network structure consists of a real input vector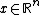 
, a hidden layer of activation functions and a linear output layer. The output of the network is a scalar function of the input vector, 
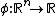, is given by
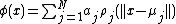
where 
is a number of neurons in the hidden layer, 
and 
are the center and weight of neuron 
. The activation function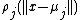 
at the HyperBF network takes the following form
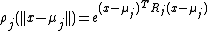
where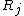 
is a positive definite 
matrix. Depending on the application, the following types of matrices 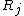are usually considered[3]
-
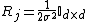, where 
. This case corresponds to the regular RBF network. -
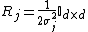, where 
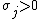. In this case, the basis functions are radially symmetric, but are scaled with different width. -
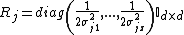, where 
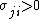. Every neuron has an elliptic shape with a varying size. - Positive definite matrix, but not diagonal.
Training
Training HyperBF networks involves estimation of weights , shape and centers of neurons 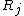and . Poggio and Girosi (1990) describe the training method with moving centers and adaptable neuron shapes. The outline of the method is provided below.
Consider the quadratic loss of the network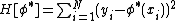 
. The following conditions must be satisfied at the optimum:
, 
, 
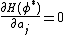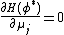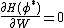
where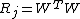 
. Then in the gradient descent method the values of 
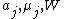that minimize 
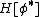can be found as a stable fixed point of the following dynamic system:
, 
, 
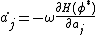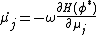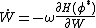
where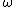 
determines the rate of convergence.
Overall, training HyperBF networks can be computationally challenging. Moreover, the high degree of freedom of HyperBF leads to overfitting and poor generalization. However, HyperBF networks have an important advantage that a small number of neurons is enough for learning complex functions.[2]
References
2. ^1 R.N. Mahdi, E.C. Rouchka (2011). "Reduced HyperBF Networks: Regularization by Explicit Complexity Reduction and Scaled Rprop-Based Training". IEEE Transactions of Neural Networks 2:673–686.
3. ^F. Schwenker, H.A. Kestler and G. Palm (2001). "Three Learning Phases for Radial-Basis-Function Network" Neural Netw. 14:439-458.
- National Accountability Bureau
- National accountability bureau
- National Accounts
- National Account Systems
- National Action Charter (Bahrain)
- National Action Charter of Bahrain
- National Action Committee on the Status of Women
- National Action (Malta)
- National Action Movement (Portugal)
- National Action Network
- National Action Party (México)
- National Action Party (Nicaragua)
- National Action Party (Turkey)
- National Action Party (UK)
- National Action Plan for Children
- National Action Plan for Salinity and Water Quality
- National Action Plan on Climate Change
- National Action Plan on the Elimination of Child Labour
- National Action (South Africa)
- National Active and Retired Federal Employees Association
- National Active Non-Commissioned Officers School (France)
- National Actors Association
- National Actors Theatre
- National address infrastructure
- National Administrative Department of Statistics