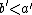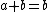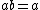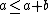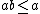“Inclusion (Boolean algebra)”的意思、由来-开放百科全书

词条

Inclusion (Boolean algebra)

释义

References

In Boolean algebra (structure), the inclusion relation 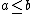is defined as 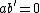and is the Boolean analogue to the subset relation in set theory. Inclusion is a partial order.

The inclusion relation can be expressed in many ways:

The inclusion relation has a natural interpretation in various Boolean algebras: in the subset algebra, the subset relation; in arithmetic Boolean algebra, divisibility; in the algebra of propositions, material implication; in the two-element algebra, the set { (0,0), (0,1), (1,1) }.

Some useful properties of the inclusion relation are:

The inclusion relation may be used to define Boolean intervals such that 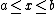A Boolean algebra whose carrier set is restricted to the elements in an interval is itself a Boolean algebra.

References

Frank Markham Brown, Boolean Reasoning: The Logic of Boolean Equations, 2nd edition, 2003, p. 52

1 : Boolean algebra

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。