- References
In mathematics, an induced character is the character of the representation V of a finite group G induced from a representation W of a subgroup H ≤ G. More generally, there is also a notion of induction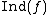 
of a class function f on H given by the formula
If f is a character of the representation W of H, then this formula for 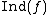calculates the character of the induced representation V of G.[1]
The basic result on induced characters is Brauer's theorem on induced characters. It states that every irreducible character on G is a linear combination with integer coefficients of characters induced from elementary subgroups.
References
1. ^{{citation | last = Serre | first = Jean-Pierre | author-link = Jean-Pierre Serre | isbn = 0-387-90190-6 | location = New York | mr = 0450380 | at = 7.2, Proposition 20 | publisher = Springer-Verlag | title = Linear Representations of Finite Groups | year = 1977}}. Translated from the second French edition by Leonard L. Scott.
{{algebra-stub}} 1 : Group theory
- Afghanistan 2009
- Afghanistan Analyst Network
- Afghanistan Analysts Network
- Afghanistan and Pakistan
- Afghanistan A tour of Pakistan in 2013
- Afghanistan at the 1951 Asian Games
- Afghanistan at the 1974 Asian Games
- Afghanistan at the 1982 Asian Games
- Afghanistan at the 1992 Summer Olympics
- Afghanistan at the 2002 Asian Games
- Afghanistan at the 2010 Asian Para Games
- Afghanistan at the 2011 World Championships in Athletics
- Afghanistan at the 2012 Summer Olympics
- Afghanistan at the 2012 Summer Paralympics
- Afghanistan at the 2013 Asian Youth Games
- Afghanistan at the 2013 World Championships in Athletics
- Afghanistan at the 2014 Asian Beach Games
- Afghanistan at the 2014 Asian Games
- Afghanistan at the 2014 Summer Youth Olympics
- Afghanistan at the Cricket World Cup
- Afghanistan-Bangladesh relations
- Afghanistan Bangladesh relations
- Afghanistan - Bangladesh relations
- Afghanistan Canada relations
- Afghanistan China relations