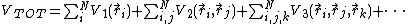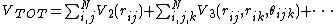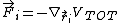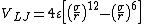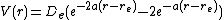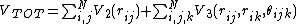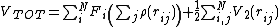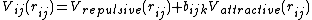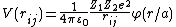- Functional form
- Force calculation
- Classes of interatomic potentials Pair potentials Many-body potentials Repulsive potentials for short-range interactions
- Potential fitting
- Reliability of interatomic potentials
- See also
- References
- External links
Functional form
Interatomic potentials can be written as a series expansion of
functional terms that depend on the position of one, two, three, etc.
atoms at a time. Then the total energy of the system V can
be written as [3]
Here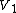 
is the one-body term, 
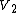the two-body term, 
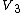the
three body term,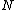 
the number of atoms in the system,
the position of atom i, etc. i, j and k are indices
that loop over atom positions.
Note that in case the pair potential is given per atom pair, in the two-body
term the potential should be multiplied by 1/2 as otherwise each bond is counted
twice, and similarly the three-body term by 1/6.[3] Alternatively,
the summation of the pair term can be restricted to cases 
and similarly for the three-body term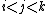 
, if
the potential form is such that it is symmetric with respect to exchange
of the j and k indices (this may not be the case for potentials
for multielemental systems).
The one-body term is only meaningful if the atoms are in an external
field (e.g. an electric field). In the absence of external fields,
the potential V should not depend on the absolute position of
atoms, but only on the relative positions. This means
that the functional form can be rewritten as a function
of interatomic distances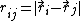 
and angles between the bonds
(vectors to neighbours)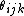 
.
Then, in the absence of external forces, the general
form becomes
In the three-body term 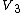the
interatomic distance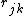 
is not needed
since the three terms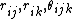 
are sufficient to give the relative positions of three atoms
i,j,k in three-dimensional space. Any terms of order higher than
2 are also called many-body potentials.
In some interatomic potentials the manybody interactions are
embedded into the terms of a pair potential (see discussion on
EAM-like and bond order potentials below).
In principle the sums in the expressions run over all N atoms.
However, if the range of the interatomic potential is finite,
i.e. the potentials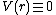 
above
some cutoff distance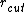 
,
the summing can be restricted to atoms within the cutoff
distance of each other. By also using a cellular method
for finding the neighbours,[1] the MD algorithm can be
an O(N) algorithm. Potentials with an infinite
range can be summed up efficiently by Ewald summation
and its further developments.
Force calculation
The forces acting between atoms can be obtained by differentiation of
the total energy with respect to atom positions. That is,
to get the force on atom i one should take the three-dimensional
derivative (gradient) with respect to the position of atom i:
For two-body potentials this gradient reduces, thanks to the
symmetry with respect to ij in the potential form, to straightforward
differentiation with respect to the interatomic distances
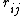. However, for many-body
potentials (three-body, four-body, etc.) the differentiation
becomes considerably more complex
[11][12]since the potential may not be any longer symmetric with respect to ij exchange.
In other words, also the energy
of atoms k that are not direct neighbours of i can depend on the position 
because of angular and other many-body terms, and hence contribute to the gradient
.
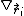Classes of interatomic potentials
Interatomic potentials come in many different varieties, with
different physical motivations. Even for single well-known elements such as silicon,
a wide variety of potentials quite different in functional form and motivation have been developed.[13]
The true interatomic interactions
are quantum mechanical in nature, and there is no known
way in which the true interactions described by
the Schrödinger equation or Dirac equation for
all electrons and nuclei could be cast into an analytical
functional form. Hence all analytical interatomic
potentials are by necessity approximations.
Pair potentials
The arguably simplest widely used interatomic interaction model is the Lennard-Jones potential
[14]
where 
is the depth of the potential well
and 
is the distance at which the potential crosses zero.
The term proportional to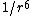 
in the potential can be motivated from a classical or quantum mechanical
description of the interaction between induced electric dipoles.[6] This
potential seems to be quite accurate for noble gases, and is widely
used for systems where dipole interactions are significant, including
in chemistry force fields to describe intermolecular interactions.
Another simple and widely used pair potential is the
Morse potential, which consists simply of a sum of two exponentials.
Here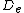 
is the equilibrium bond energy and
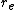the bond distance. The Morse
potential has been applied to studies of molecular vibrations and solids
,[15] and although rarely used anymore, inspired the functional form
of more modern potentials such as the bond-order potentials.
Ionic materials are often described by a sum of a
short-range repulsive term, such as the
Buckingham pair potential, and a long-range Coulomb potentialgiving the ionic interactions between the ions forming the material. The short-range
term for ionic materials can also be of many-body character
.[16]
Pair potentials have some inherent limitations, like the inability
to describe all 3 elastic constants of
cubic metals.[7] Hence modern molecular dynamics simulations
are to a large extent carried out with different kinds of many-body potentials.
Many-body potentials
The Stilinger-Weber potential[17] is a potential that has a
two-body and three-body terms of the standard form
where the three-body term describes how the potential energy changes with bond bending.
It was originally developed for pure Si, but has been extended to many other
elements and compounds
[18][19]and also formed the basis for other Si potentials.[20]
[21]Metals are very commonly described with what can be called
"EAM-like" potentials, i.e. potentials that share
the same functional form as the embedded atom model.
In these potentials, the total potential energy is written
where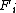 
is a so-called embedding function
(not to be confused with the force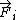 
) that is a function of the sum of the so-called electron density
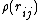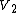
. is a pair potential that usually is purely repulsive. In the original
formulation [22] the electron
density function 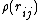was obtained
from true atomic electron densities, and the embedding function
was motivated from density-functional theory as the energy needed
to 'embed' an atom into the electron density.
.[23]
However, many other potentials used for metals share the same functional
form but motivate the terms differently, e.g. based
on tight-binding theory
[24][25]or other motivations
[26][27].[28]
EAM-like potentials are usually implemented as numerical tables.
A collection of tables is available at the interatomic
potential repository at NIST
Covalently bonded materials are often described by
bond order potentials, sometimes also called
Tersoff-like or Brenner-like potentials.
[10][29][30]These have in general a form that resembles a pair potential:
where the repulsive and attractive part are simple exponential
functions similar to those in the Morse potential.
However, the strength is modified by the environment of the atom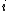 
via the 
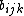term. If implemented without
an explicit angular dependence, these potentials
can be shown to be mathematically equivalent to
some varieties of EAM-like potentials
[31][32]Thanks to this equivalence, the bond-order potential formalism has been implemented also for many metal-covalent mixed materials.[32][33]
[34][35]Repulsive potentials for short-range interactions
For very short interatomic separations, important in radiation material science,
the interactions can be described quite accurately with screened Coulomb potentials which have the general form
here φ(r) → 1 when r → 0. Here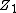 
and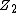 
are the charges of the interacting nuclei, and a is the so-called screening parameter.
A widely used popular screening function is the "Universal ZBL" one.[36]
and more accurate ones can be obtained from all-electron quantum chemistry calculations
[37]In binary collision approximation simulations this kind of potential can be used
to describe the nuclear stopping power.
Potential fitting
Since the interatomic potentials are approximations, they by necessity all involve
parameters that need to be adjusted to some reference values. In simple
potentials such as the Lennard-Jones and Morse ones, the parameters can be
set directly to match e.g. the equilibrium bond length and bond strength
of a dimer molecule or the cohesive energy of a solid
.[6] However, many-body
potentials often contain tens or even hundreds of adjustable parameters.
These can be fit into a larger set of experimental data, or materials
properties derived from more fundamental simulation models such as
density-functional theory. For solids, a well-constructed many-body potential
can often describe at least the equilibrium crystal structure cohesion and
lattice constant, linear elastic constants, and
basic point defect properties of all the elements and stable compounds well.
[21][32][34][35][38][39].[40]
The aim of most potential construction and fitting is to make the potential
transferable, i.e. that it can describe materials properties that are clearly
different from those it was fitted to (for examples of potentials explicitly aiming for this,
see e.g.[41][42]). As an example of demonstrated
partial transferability, a review of interatomic potentials
of Si found that for instance the Stillinger-Weber and Tersoff III potentials for Si
are indeed able to describe several (but certainly not all) materials properties they were not fitted to
.[13]
The NIST interatomic potential repository provides
a collection of fitted interatomic potentials, either as fitted parameter values or numerical
tables of the potential functions.[43]
Reliability of interatomic potentials
Classical interatomic potentials cannot reproduce all phenomena. Sometimes quantum description is necessary. Density functional theory is used to overcome this limitation.
See also
- Molecular dynamics
- Bond order potential
- Effective medium theory
- Embedded atom model
- Lennard-Jones potential
- Buckingham potential
- ReaxFF
- Force field (chemistry)
References
2. ^Daan Frenkel and Berend Smit. Understanding molecular simulation: from algorithms to applications. Academic Press, San Diego, second edition, 2002.
3. ^1 2 R. Lesar. Introduction to Computational Materials Science. Cambridge University Press, 2013.
4. ^D. W. Brenner. The art and science of an analytical potential. Physica Status Solidi B, 217:23, 2000
5. ^N. W. Ashcroft and N. D. Mermin. Solid State Physics.Saunders College, Philadelphia, 1976.
6. ^1 2 Charles Kittel. Introduction to Solid State Physics. John Wiley & Sons, New York, third edition, 1968.
7. ^1 Murray S. Daw, Stephen M. Foiles, and Micael I. Baskes. The embedded-atom method: a review of theory and applications, Mat. Sci. Rep., 9:251, 1993.
8. ^J. Tersoff. New Empirical approach for the structure and energy of covalent systems. Phys. Rev. B, 37:6991, 1988
9. ^M. W. Finnis, Bond-order potentials through the ages,Progress in Materials Science 52 (2007) 133
10. ^1 Sinnott, S.B., Brenner, D.W. (2012) Three decades of many-body potentials in materials research. MRSBulletin 37: 469-473
11. ^K. M. Beardmore and N. Gr/onbech-Jensen. Direct simulation of ion beam induced stressing and amorphization of silicon. Phys. Rev. B, 60:12610, 1999.
12. ^K. Albe, J. Nord, and K. Nordlund. Dynamic charge-transfer bond-order potential for gallium nitride. Phil. Mag. A, 89:3477--3497, 2009.
13. ^1 H. Balamane, T. Halicioglu, and W. A. Tiller. Comparative study of silicon empirical interatomic potentials. Phys. Rev. B, 46(4):2250, 1992.
14. ^{{Citation |last=Lennard-Jones |first=J. E. |year=1924 |title=On the Determination of Molecular Fields |journal=Proc. R. Soc. Lond. A |volume=106 |issue=738 |pages=463–477 |doi=10.1098/rspa.1924.0082 |bibcode = 1924RSPSA.106..463J }}.
15. ^L. A. Girifalco and V. G. Weizer. Application of the Morse potential function to cubic metals. Phys. Rev., 114(3):687, 1959.
16. ^B. P. Feuston and S. H. Garofalini. Empirical three-body potential for vitreous silica. J. Chem. Phys., 89(9):5818, 1988.
17. ^F. H. Stillinger and T. A. Weber. Computer simulation of local order in condensed phases of silicon. Phys. Rev. B, 31:5262, 1985
18. ^M. Ichimura. Stillinger-weber potentials for iii-v compound semiconductors and their application to the critical thickness calculation for inas/gaas. Physica Status Solidi A, 153(2):431--7, 1996.
19. ^H. Ohta and S. Hamaguchi. Classical interatomic potentials for si-o-f and si-o-cl systems. J. Chemical Physics, 115(14):6679--90, 2001.
20. ^{{cite journal|last1=Bazant|first1=M. Z.|last2=Kaxiras|first2=E.|last3=Justo|first3=J. F.|title=Environment-dependent interatomic potential for bulk silicon|journal=Phys. Rev. B|date=1997|volume=56|issue=14|page=8542|doi=10.1103/PhysRevB.56.8542|arxiv=cond-mat/9704137|bibcode=1997PhRvB..56.8542B}}
21. ^1 J. F. Justo, M. Z. Bazant, E. Kaxiras, V. V. Bulatov, and S. Yip.Interatomic potential for silicon defects and disordered phases. Phys. Rev. B, 58:2539, 1998.
22. ^S. M. Foiles, M. I. Baskes, andM. S. Daw. Embedded-atom-method functions for the fcc metals cu, ag,au, ni, pd, pt, and their alloys. Phys. Rev. B, 33(12):7983,1986. Erratum: ibid, Phys. Rev. B 37, 10378 (1988).
23. ^M. J. Puska, R. M. Nieminen, and M. Manninen. Atoms embedded in an electron gas: Immersion energies. Phys. Rev. B, 24(6):3037, 1981.
24. ^M. W. Finnis and J. E. Sinclair. A simple empirical n-body potential for transition metals. Phil. Mag. A, 50(1):45, 1984. see also Erratum, ibid. 53 (1986) 161.
25. ^F. Cleri and V. Rosato. Tight-binding potentials for transition metals and alloys. Phys. Rev. B, 48(1):22, 1993.
26. ^C. L. Kelchner, D. M. Halstead, L. S. Perkins, N. M. Wallace, and A. E. DePristo. Construction and evaluation of embedding functions. Surf. Sci., 310:425--435, 1994. and references therein.
27. ^S. L. Dudarev and P. M. Derlet. A magnetic interatomic potential for molecular dynamics simulations. J. Phys.: Condens. Matter, 17:1--22, 2005.
28. ^P. Olsson, J. Wallenius, C. Domain, K. Nordlund, and L. Malerba. Two-band modeling of alpha-prime phase formation in Fe-Cr. Phys. Rev. B, 72:214119, 2005.
29. ^{{cite journal|last1=Tersoff|first1=J.|title=New empirical approach for the structure and energy of covalent systems|journal=Physical Review B|volume=37|issue=12|year=1988|pages=6991–7000|issn=0163-1829|doi=10.1103/PhysRevB.37.6991|bibcode=1988PhRvB..37.6991T}}
30. ^{{cite journal|last1=Brenner|first1=Donald W.|title=Empirical potential for hydrocarbons for use in simulating the chemical vapor deposition of diamond films|journal=Physical Review B|volume=42|issue=15|year=1990|pages=9458–9471|issn=0163-1829|doi=10.1103/PhysRevB.42.9458|bibcode=1990PhRvB..42.9458B}}
31. ^{{cite journal|last1=Brenner|first1=Donald W.|title=Relationship between the embedded-atom method and Tersoff potentials|journal=Physical Review Letters|volume=63|issue=9|year=1989|pages=1022|issn=0031-9007|doi=10.1103/PhysRevLett.63.1022|pmid=10041250|bibcode=1989PhRvL..63.1022B}}
32. ^1 2 {{cite journal|last1=Albe|first1=Karsten|last2=Nordlund|first2=Kai|last3=Averback|first3=Robert S.|title=Modeling the metal-semiconductor interaction: Analytical bond-order potential for platinum-carbon|journal=Physical Review B|volume=65|issue=19|pages=195124|year=2002|issn=0163-1829|doi=10.1103/PhysRevB.65.195124|bibcode=2002PhRvB..65s5124A}}
33. ^{{cite journal|last1=de Brito Mota|first1=F.|last2=Justo|first2=J. F.|last3=Fazzio|first3=A.|title=Structural properties of amorphous silicon nitride|journal=Phys. Rev. B|date=1998|volume=58|issue=13|page=8323|doi=10.1103/PhysRevB.58.8323|bibcode=1998PhRvB..58.8323D}}
34. ^1 N. Juslin, P. Erhart, P. Träskelin, J. Nord, K. O. E. Henriksson, K. Nordlund, E. Salonen, and K. Albe. Analytical interatomic potential for modelling non-equilibrium processes in the w-c-h system. J. Appl. Phys., 98:123520, 2005.
35. ^1 Paul Erhart, Niklas Juslin, Oliver Goy, Kai Nordlund, Ralf Muller, and Karsten Albe. Analytic bond-order potential for atomistic simulations of zinc oxide. J. Phys.: Condens. Matter, 18:6585--6605, 2006.
36. ^J. F. Ziegler, J. P. Biersack, and U. Littmark. The Stopping and Range of Ions in Matter. Pergamon, New York, 1985.
37. ^K. Nordlund, N. Runeberg, and D. Sundholm. Repulsive interatomic potentials calculated using hartree-fock and density-functional theory methods. Nucl. Instrum. Methods Phys. Res. B, 132:45--54, 1997.
38. ^Furio Ercolessi and J. B. Adams. Interatomic potentials from first-principles calculations: the force-matching method. Europhys. Lett., 26:583, 1994.
39. ^Y. Mishin, M. J. Mehl, and D. A. Papaconstantpoulos. Embedded-atom potential for b2-NiAl. Phys. Rev. B, 65:224114, 2002.
40. ^Keith Beardmore and Roger Smith. Empirical potentials for c-si-h systems with application to c60 interactions with si crystal surfaces. Phil. Mag. A, 74:1439--1466, 1996.
41. ^Varghese Swamy and Julian D. Gale, Transferable variable-charge interatomic potential for atomistic simulation of titanium oxides, Phys. Rev. B 62 (2000) 5406
42. ^Andrés Aguado, Leonardo Bernasconi, Paul A. Madden, A transferable interatomic potential for MgO from ab initio molecular dynamics, Chem. Phys. Lett. 356 (2002) 437
43. ^{{cite web|url=http://www.ctcms.nist.gov/potentials/|title=Interatomic Potentials Repository Project|first=U.S. Department of Commerce, National Institute of Standards and|last=Technology|website=www.ctcms.nist.gov}}
External links
- NIST interatomic potential repository
- [https://www.ctcms.nist.gov/~knc6/periodic.html NIST JARVIS-FF]