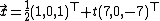请输入您要查询的百科知识：

　

词条 Intersection curve
释义

  1. Intersection line of two planes

  2. Intersection curve of a plane and a quadric

  3. Intersection curve of a cylinder or cone and a quadric

  4. General case: marching method

  5. Application: contour line

  6. Intersection curve of two polyhedrons

  7. See also

  8. References

In geometry, an intersection curve is, in the most simple case, the intersection line of two non-parallel planes in Euclidean 3-space. In general, an intersection curve consists of the common points of two transversally intersecting surfaces, meaning that at any common point the surface normals are not parallel. This restriction excludes cases where the surfaces are touching or have surface parts in common.

The analytic determination of the intersection curve of two surfaces is easy only in simple cases; for example: a) the intersection of two planes, b) plane section of a quadric (sphere, cylinder, cone, etc.), c) intersection of two quadrics in special cases. For the general case, literature provides algorithms, in order to calculate points of the intersection curve of two surfaces.[1]

Intersection line of two planes

Given: two planes 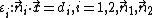linearly independent, i.e. the planes are not parallel.

Wanted: A parametric representation 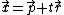of the intersection line.

The direction of the line one gets from the crossproduct of the normal vectors: .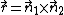

A point 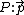of the intersection line can be determined by intersecting the given planes 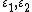with the plane 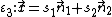, which is perpendicular to and 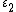. Inserting the parametric representation of 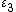into the equations of und 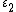yields the parameters und .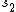

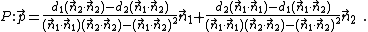Example: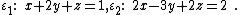

The normal vectors are 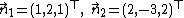and the direction of the intersection line is 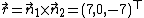. For point 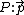, one gets from the formula abov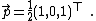e Hence

is a parametric representation of the line of intersection.

Remarks:
  1. In special cases, the determination of the intersection line by the Gaussian elimination may be faster.
  2. If one (or both) of the planes is given parametrically by 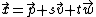, one gets 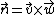as normal vector and the equation is: .

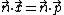Intersection curve of a plane and a quadric

In any case, the intersection curve of a plane and a quadric (sphere, cylinder, cone,...) is a conic section. For details, see.[2] An important application of plane sections of quadrics is contour lines of quadrics. In any case (parallel or central projection), the contour lines of quadrics are conic sections. See below and Umrisskonstruktion.

Intersection curve of a cylinder or cone and a quadric

It is an easy task to determine the intersection points of a line with a quadric (i.e. line-sphere); one only has to solve a quadratic equation. So, any intersection curve of a cone or a cylinder (they are generated by lines) with a quadric consists of intersection points of lines and the quadric (see pictures).

The pictures show the possibilities which occur when intersecting a cylinder and a sphere:

  1. In the first case, there exists just one intersection curve.
  2. The second case shows an example where the intersection curve consists of two parts.
  3. In the third case, the sphere and cylinder touch each other at one singular point. The intersection curve is self-intersecting.
  4. If the cylinder and sphere have the same radius and the midpoint of the sphere is located on the axis of the cylinder, then the intersection curve consists of singular points (a circle) only.

General case: marching method

In general, there are no special features to exploit. One possibility to determine a polygon of points of the intersection curve of two surfaces is the marching method (see section References). It consists of two essential parts:

  1. The first part is the curve point algorithm, which determines to a starting point in the vicinity of the two surfaces a point on the intersection curve. The algorithm depends essentially on the representation of the given surfaces. The simplest situation is where both surfaces are implicitly given by equations 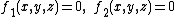, because the functions provide information about the distances to the surfaces and show via the gradients the way to the surfaces. If one or both the surfaces are parametrically given, the advantages of the implicit case do not exist. In this case, the curve point algorithm uses time-consuming procedures like the determination of the footpoint of a perpendicular on a surface.
  2. The second part of the marching method starts with a first point on the intersection curve, determines the direction of the intersection curve using the surface normals, then makes a step with a given step length into the direction of the tangent line, in order to get a starting point for a second curve point, ... (see picture).

For details of the marching algorithm, see.[3]

The marching method produces for any starting point a polygon on the intersection curve. If the intersection curve consists of two parts, the algorithm has to be performed using a second convenient starting point. The algorithm is rather robust. Usually, singular points are no problem, because the chance to meet exactly a singular point is very small (see picture: intersection of a cylinder and the surface ).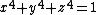

Application: contour line

A point of the contour line of an implicit surface with equation 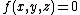and parallel projection with direction has to fulfill the condition 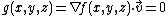, because 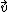has to be a tangent vector, which means any contour point is a point of the intersection curve of the two implicit surfaces

.

For quadrics, is always a linear function. Hence the contour line of a quadric is always a plane section (i.e. a conic section).

The contour line of the surface 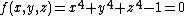(see picture) was traced by the marching method.

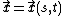Remark: The determination of a contour polygon of a parametric surface needs tracing an implicit curve in parameter plane.[4]

Condition for contour points: .

Intersection curve of two polyhedrons

The intersection curve of two polyhedrons is a polygon (see intersection of three houses). The display of a parametrically defined surface is usually done by mapping a rectangular net into 3-space. The spatial quadrangles are nearly flat. So, for the intersection of two parametrically defined surfaces, the algorithm for the intersection of two polyhedrons can be used.[5] See picture of intersecting tori.

{{-}}

See also

  • Intersection point

References

1. ^Geometry and Algorithms for COMPUTER AIDED DESIGN, p. 94
2. ^CDKG: Computerunterstützte Darstellende und Konstruktive Geometrie (TU Darmstadt) (PDF; 3,4 MB), p. 87–124
3. ^Geometry and Algorithms for COMPUTER AIDED DESIGN, p. 94
4. ^Geometry and Algorithms for COMPUTER AIDED DESIGN, p. 99
5. ^Geometry and Algorithms for COMPUTER AIDED DESIGN p. 76
  • C:L: Bajaj, C.M. Hoffmann, R.E. Lynch: Tracing surface intersections, Comp. Aided Geom. Design 5 (1988), p. 285-307.
  • R.E. Barnhill, S.N. Kersey: AMarching method for parametric surface/surface intersection, Comp. Aided Geom. Design 7 (1990), p. 257-280.
  • R. Barnhill, G. Farin, M. Jordan, B. Piper: Surface/Surface intersection, Computer Aided Geometric Design 4 (1987), p 3-16.

2 : Euclidean geometry|Linear algebra
随便看

　

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。

　

Copyright © 2023 OENC.NET All Rights Reserved
京ICP备2021023879号 更新时间：2024/11/15 13:21:01