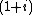“Rudvalis group”的意思、由来-开放百科全书

词条

Rudvalis group

释义

History
Properties
Maximal subgroups
References
External links

In the area of modern algebra known as group theory, the Rudvalis group Ru is a sporadic simple group of order

2¹⁴{{·}}3³{{·}}5³{{·}}7{{·}}13{{·}}29

= 145926144000

≈ 1{{e|11}}.

History

Ru is one of the 26 sporadic groups and was found by {{Harvard citations |last=Rudvalis |first=Arunas |author-link=Arunas Rudvalis |year=1973 |year2=1984 |txt=yes}} and constructed by {{Harvard citations |last1 = Conway|first1 = John H.|author1-link = John H. Conway|last2 = Wales|first2 = David B.|year=1973 |txt=yes}}. Its Schur multiplier has order 2, and its outer automorphism group is trivial.

In 1982 Robert Griess showed that Ru cannot be a subquotient of the monster group.^[1] Thus it is one of the 6 sporadic groups called the pariahs.

Properties

The Rudvalis group acts as a rank 3 permutation group on 4060 points, with one point stabilizer being the Ree group

²F₄(2), the automorphism group of the Tits group. This representation implies a strongly regular graph srg(4060, 2304, 1328, 1208), i.e. each vertex has 2304 neighbors and 1755 non-neighbors, any two adjacent vertices have 1328 common neighbors, while any two non-adjacent ones have 1208 {{Harvard citations|last=Griess|year=1998|loc=p. 125}}.

Its double cover acts on a 28-dimensional lattice over the Gaussian integers. The lattice has 4×4060 minimal vectors; if minimal vectors are identified whenever one is 1, i, –1, or –i times another, then the 4060 equivalence classes can be identified with the points of the rank 3 permutation representation. Reducing this lattice modulo the principal ideal

gives an action of the Rudvalis group on a 28-dimensional vector space over the field 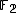with 2 elements. Duncan (2006) used the 28-dimensional lattice to construct a vertex operator algebra acted on by the double cover.

{{harvtxt|Parrott|1976}} characterized the Rudvalis group by the centralizer of a central involution. {{harvtxt|Aschbacher|Smith|2004}} gave another characterization as part of their identification of the Rudvalis group as one of the quasithin groups.

Maximal subgroups

{{harvtxt|Wilson|1984}} found the 15 conjugacy classes of maximal subgroups of Ru as follows:

²F₄(2) = ²F₄(2)'.2
2⁶.U₃(3).2
(2² × Sz(8)):3
2³⁺⁸:L₃(2)
U₃(5):2
2¹⁺⁴⁺⁶.S₅
PSL₂(25).2²
A₈
PSL₂(29)
5²:4.S₅
3.A₆.2²
5¹⁺²:[2⁵]
L₂(13):2
A₆.2²
5:4 × A₅

References

1. ^Griess (1982)

{{Citation | last1=Aschbacher | first1=Michael | author1-link=Michael Aschbacher | last2=Smith | first2=Stephen D. | title=The classification of quasithin groups. I Structure of Strongly Quasithin K-groups | url=http://www.ams.org/bookstore-getitem/item=SURV-111 | publisher=American Mathematical Society | location=Providence, R.I. | series=Mathematical Surveys and Monographs | isbn=978-0-8218-3410-7 | mr=2097623 | year=2004 | volume=111}}
{{Citation

|last1 = Conway
|first1 = John H.
|author1-link = John H. Conway
|last2 = Wales
|first2 = David B.
|title = The construction of the Rudvalis simple group of order 145926144000
|journal = Journal of Algebra
|issue = 3
|year = 1973
|pages = 538–548
|doi = 10.1016/0021-8693(73)90063-X
|volume = 27
}}

{{cite arXiv

|author = John F. Duncan
|title = Moonshine for Rudvalis's sporadic group
|year = 2008
|eprint = math/0609449v1
}}

{{Citation

|last = Griess
|first = Robert L.
|author-link = Robert Griess
|title = The Friendly Giant
|journal = Inventiones Mathematicae
|issue = 1
|year = 1982
|pages = 1–102
|doi = 10.1007/BF01389186
|volume = 69
|bibcode = 1982InMat..69....1G
}}

{{Citation

|last = Griess
|first = Robert L.
|title = Twelve Sporadic Groups
|year = 1998
|publisher = Springer-Verlag
}}

{{Citation | last1=Parrott | first1=David | title=A characterization of the Rudvalis simple group | doi=10.1112/plms/s3-32.1.25 | mr=0390043 | year=1976 | journal=Proceedings of the London Mathematical Society |series=Third Series | issn=0024-6115 | volume=32 | issue=1 | pages=25–51}}
{{Citation

|last = Rudvalis
|first = Arunas
|author-link = Arunas Rudvalis
|title = A new simple group of order 2¹⁴ 3³ 5³ 7 13 29
|journal = Notices of the American Mathematical Society
|issue = 20
|year = 1973
|pages = A–95
}}

{{Citation | last1=Rudvalis | first1=Arunas | title=A rank 3 simple group of order 2¹⁴3³5³7.13.29. I | doi=10.1016/0021-8693(84)90063-2 |mr=727376 | year=1984 | journal=Journal of Algebra | issn=0021-8693 | volume=86 | issue=1 | pages=181–218}}
{{Citation | last1=Rudvalis | first1=Arunas | title=A rank 3 simple group G of order 2¹⁴3³5³7.13.29. II. Characters of G and Ĝ | doi=10.1016/0021-8693(84)90064-4 |mr=727377 | year=1984 | journal=Journal of Algebra | issn=0021-8693 | volume=86 | issue=1 | pages=219–258}}
{{Citation | last1=Wilson | first1=Robert A. | title=The geometry and maximal subgroups of the simple groups of A. Rudvalis and J. Tits | doi=10.1112/plms/s3-48.3.533 | mr=735227 | year=1984 | journal=Proceedings of the London Mathematical Society |series=Third Series | issn=0024-6115 | volume=48 | issue=3 | pages=533–563}}

External links

MathWorld: Rudvalis Group
Atlas of Finite Group Representations: Rudvalis group

1 : Sporadic groups

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。