“Jacobi set”的意思、由来-开放百科全书

词条

Jacobi set

释义

Definition
References

{{Multiple issues|{{orphan|date=September 2011}}{{one source|date=August 2011}}{{expert-subject|date=August 2011}}
}}

In Morse theory, a mathematical discipline, Jacobi sets provide a method of studying the relationship between two or more Morse functions.

For two Morse functions, the Jacobi set is defined as the set of critical points of the restriction of one function to the level sets of the other function.^[1]

The Jacobi set can also be defined as the set of points where the gradients of the two functions are parallel.

If both the functions are generic, the Jacobi set is a smoothly embedded 1-manifold.

Definition

Consider two generic Morse functions defined on a smooth -manifold. Let the restriction of to the level set for a regular value, be called ; it is a Morse function. Then the Jacobi set of and is ,

Alternatively, the Jacobi set is the collection of points where the gradients of the functions align with each other or one of the gradients vanish (cite?), for some ,

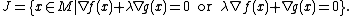
Equivalently, the Jacobi set can be described as the collection of critical points of the family of functions 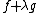, for some ,

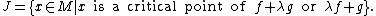
References

1. ^{{cite journal|last=Edelsbrunner|first=Herbert|author2=John Harer|year=2002|title=Jacobi sets of multiple morse functions|journal=Foundations of Computational Mathematics|publisher=Cambridge University Press|pages=37–57}}

1 : Morse theory

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。