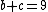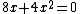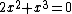1. Introduction
    The Unitary Nebuls   The Mystery of Two Natures   The Evolution of Three Talents   Simultaneous of the Four Elements  

2. Book I
    Problems of Right Angle Triangles and Rectangles  Problems of Plane Figures  Problems of Piece Goods  Problems on Grain Storage  Problems on Labour  Problems of Equations for Fractional Roots 

3. Book II
    Mixed Problems  Containment of Circles and Squares  Problems on Areas  Surveying with Right Angle Triangles  Hay Stacks  Bundles of Arrows  Land Measurement  Summon Men According to Need 

4. Book III
    Fruit pile  Figures within Figure  Simultaneous Equations  Equation of two unknowns  Left and Right  Equation of Three Unknowns  Equation of Four Unknowns 

5. References

Jade Mirror of the Four Unknowns,^[1] Siyuan yujian ({{lang|zh|四元玉鉴}}), also referred to as Jade Mirror of the Four Origins,^[2] is a 1303 mathematical monograph by Yuan dynasty mathematician Zhu Shijie.^[3] With this masterpiece, Zhu brought Chinese algebra to its highest level.

The book consists of an introduction and three books, with a total of 288 problems. The first four problems in the introduction illustrate his method of the four unknowns. He showed how to convert a problem stated verbally into a system of polynomial equations (up to the 14th order), by using up to four unknowns: 天Heaven, 地Earth, 人Man, 物Matter, and then how to reduce the system to a single polynomial equation in one unknown by successive elimination of unknowns. He then solved the high-order equation by Southern Song dynasty mathematician Qin Jiushao's "Ling long kai fang" method published in Shùshū Jiǔzhāng (“Mathematical Treatise in Nine Sections”) in 1247 (more than 570 years before English mathematician William Horner's method using synthetic division). To do this, he makes use of the Pascal triangle, which he labels as the diagram of an ancient method first discovered by Jia Xian before 1050.

Zhu also solved square and cube roots problems by solving quadratic and cubic equations, and added to the understanding of series and progressions, classifying them according to the coefficients of the Pascal triangle. He also showed how to solve systems of linear equations by reducing the matrix of their coefficients to diagonal form. His methods predate Blaise Pascal, William Horner, and modern matrix methods by many centuries. The preface of the book describes how Zhu travelled around China for 20 years as a teacher of mathematics.

Jade Mirror of the Four Unknowns consists of four books, with 24 classes and 288 problems, in which 232 problems deal with Tian yuan shu, 36 problems deal with variable of two variables, 13 problems of three variables, and 7 problems of four variables.

Introduction

The four quantities are x, y, z, w can be presented with the following diagram

{{v1}}x

y{{v1}} {{Rod0}}太{{v1}}w

{{v1}}z

The square of which is:

The Unitary Nebuls

This section deals with Tian yuan shu or problems of one unknown.

Question: Given the product of huangfan and zhi ji equals to 24 paces, and the sum of vertical and hypothenus equals to 9 paces, what is the value of the base?

Answer: 3 paces

Set up unitary tian as the base( that is let the base be the unknown quantity x)

Since the product of huangfang and zhi ji = 24

in which

huangfan is defined as：^[4]

zhi ji：

therefore

Further, the sum of vertical and hypothenus is

Set up the unknown unitary tian as the vertical

We obtain the following equation

{{v3}}{{h8}}{{v-8}}{{h8}} （）

{{Rod0}} 太

{{v7}}{{h2}}{{v9}}

{{v-8}}{{h1}}

{{v-9}}

{{v1}}

Solve it and obtain x=3

The Mystery of Two Natures

{{v-2}}{{Rod0}}太 Unitary

{{v-1}}{{Rod2}}{{Rod0}}

{{Rod0}}{{Rod2}}{{Rod0}}

{{Rod0}}{{Rod0}}{{v1}}

equation： ;

from the given

{{Rod2}}{{Rod0}}太

{{v-1}}{{Rod2}}{{Rod0}}

{{Rod0}}{{Rod0}}{{Rod0}}

{{Rod0}}{{Rod0}}{{v1}}

equation： ;

we get：

太

{{v'8}}

{{v4}}

and

太

{{Rod0}}

{{Rod2}}

{{v1}}

by method of elimination, we obtain a quadratic equation

{{v-8}}

{{v-2}}

{{v1}}

solution: 。

The Evolution of Three Talents

Template for solution of problem of three unknowns

Zhu Shijie explained the method of elimination in detail. His example has been quoted frequently in scientific literature^[5][6][7]。

Set up three equations as follows

{{v-1}}太{{v-1}}

{{v1}}

{{v-1}}{{Rod0}}{{v-1}}

.... I

{{v-1}}{{Rod0}}{{v-1}}

{{v1}}

{{v-1}}

.....II

{{v1}}{{Rod0}}太{{Rod0}}{{v-1}}

{{Rod0}}

{{v1}}

....III

Elimination of unknown between II and III

by manipulation of exchange of variables

We obtain

{{v1}} {{v1}}{{v-2}}太

{{v-1}}{{v1}}{{v-1}}

{{Rod0}}{{v1}}{{v-2}}

...IV

and

{{v1}}{{v-2}}{{Rod2}}太

{{Rod0}}{{v-2}}{{v4}}{{v-2}}

{{Rod0}}{{Rod0}}{{v1}}{{v-2}}

.... V

Elimination of unknown between IV and V we obtain a 3rd order equation

{{v-5}}

{{v6}}

{{v4}}

{{v-6}}

{{v1}}

Solve to this 3rd order equation to obtain ；

Change back the variables

We obtain the hypothenus =5 paces

Simultaneous of the Four Elements

This section deals with simultaneous equations of four unknowns。

Successive elimination of unknowns to get

{{h6}}{{v'8}}{{h-6}}

{{v-7}}

{{v4}}

Solve this and obtain 14 paces

Book I

Problems of Right Angle Triangles and Rectangles

There are 18 problems in this section.

Problem 18

Obtain a tenth order polynomial equation:

The root of which is x = 3， multiply by 4, getting 12. That is the final answer。

Problems of Plane Figures

There are 18 problems in this section

Problems of Piece Goods

There are 9 problems in this section

Problems on Grain Storage

There are 6 problems in this section

Problems on Labour

There are 7 problems in this section

Problems of Equations for Fractional Roots

There are 13 problems in this section

Book II

Mixed Problems

Containment of Circles and Squares

Problems on Areas

Surveying with Right Angle Triangles

There are eight problems in this section

Problem 1

Answer: 120 paces in length and width one li}}

Let tian yuan unitary as half of the length, we obtain a 4th order equation

^[8]

solve it and obtain {{mvar|x}}=240 paces，hence length =2x= 480 paces=1 li and 120paces。

Similarity, let tian yuan unitary(x) equals to half of width

we get the equation：

^[9]

Solve it to obtain {{mvar|x}}=180 paces，length =360 paces =one li。

Problem 7

Identical to The depth of a ravine (using hence-forward cross-bars) in Haidao Suanjing.

Problem 8

Identical to The depth of a transparent pool in Haidao Suanjing.

Hay Stacks

Bundles of Arrows

Land Measurement

Summon Men According to Need

Problem No 5 is the earliest 4th order interpolation formula in the world

men summoned :^[10]

In which

• {{mvar|a}}=1st order difference
• {{mvar|b}}=2nd order difference
• {{mvar|c}}=3rd order difference
• {{mvar|d}}=4th order difference

Book III

Fruit pile

This section contains 20 problems dealing with triangular piles, rectangular piles

Problem 1

Find the sum of triangular pile

and value of the fruit pile is:

Zhu Shijie use Tian yuan shu to solve this problem by letting x=n

and obtained the formular

From given condition 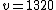, hence

^[11]

Solve it to obtain 。

Therefore,

。

Figures within Figure

Simultaneous Equations

Equation of two unknowns

Left and Right

Equation of Three Unknowns

Equation of Four Unknowns

Six problems of four unknowns。

Question 2

Yield a set of equations in four unknowns：.^[12]

References

• Jade Mirror of the Four Unknowns, tr. into English by Professor Chen Zhaixin, Former Head of Mathematics Department, Yenching University (in 1925),Translated into modern Chinese by Guo Shuchun, Volume I & II, Library of Chinese Classics, Chinese-English, Liaoning Education Press 2006 {{isbn|7-5382-6923-1}} https://www.scribd.com/document/357204551/Siyuan-yujian-2, https://www.scribd.com/document/357204728/Siyuan-yujian-1
• Collected Works in the History of Sciences by Li Yan and Qian Baocong, Volume 1 《李俨钱宝琮科学史全集》 第一卷 钱宝琮 《中国算学史 上编》
• Zhu Shijie Siyuan yujian Book 1-4, Annotated by Qin Dyasty mathematician Luo Shilin, Commercial Press
• J. Hoe, Les systèmes d'équations polynômes dans le Siyuan yujian (1303), Institut des Hautes Études Chinoises, Paris, 1977
• J. Hoe, A study of the fourteenth-century manual on polynomial equations "The jade mirror of the four unknowns" by Zhu Shijie, Mingming Bookroom, P.O. Box 29-316, Christchurch, New Zealand, 2007

• Daud Haider
• Daud Halt railway station
• Daudhar
• Da'ud ibn Isa
• Da'udi Bohra
• Daudin's bronzeback
• Daudi Ocheng
• Daudi Ochieng
• Daud Jumbish
• Daud Junbish
• Daud Khel-Lakki Marwat Branch Line
• Daud Khel–Lakki Marwat Branch Line
• Daud, Mohammad
• Daudov
• Daudova
• Daudov Magomed
• Daud Public School And College
• Daud Public School and College
• Daudpur
• Daudpur Bazar
• Daudpur, Kapurthala
• Daudpur Siksha Sadan
• Daud Shah of Gujarat
• Daudsu Jamaluddin
• Dauenhauer, Richard