1. Jantzen filtration for Verma modules

2. References

In algebra, a Jantzen filtration is a filtration of a Verma module of a semisimple Lie algebra, or a Weyl module of a reductive algebraic group of positive characteristic. Jantzen filtrations were introduced by {{harvs|txt|author-link=Jens Carsten Jantzen|last=Jantzen|year=1979}}.

Jantzen filtration for Verma modules

If M(λ) is a Verma module of a semisimple Lie algebra with highest weight λ, then the Janzen filtration is a decreasing filtration

It has the following properties:

• M(λ)¹ is the maximal proper submodule of M(λ)
• The quotients M(λ)^k/M(λ)^k+1 have non-degenerate contravariant bilinear forms.
• 

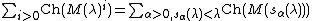
(the Jantzen sum formula)

References

• {{Citation | last1=Beilinson | first1=A. A. | author1-link=Alexander Beilinson | last2=Bernstein | first2=Joseph | author2-link=Joseph Bernstein | editor1-last=Gelʹfand | editor1-first=Sergei | editor2-last=Gindikin | editor2-first=Simon | title= I. M. Gelʹfand Seminar | url=http://www.math.harvard.edu/~gaitsgde/grad_2009/BB%20-%20Jantzen.pdf | publisher=American Mathematical Society | location=Providence, R.I. | series=Adv. Soviet Math. | isbn=978-0-8218-4118-1 | year=1993 | volume=16 | chapter=A proof of Jantzen conjectures | pages=1–50}}
• {{Citation | last1=Humphreys | first1=James E. | title=Representations of semisimple Lie algebras in the BGG category O | url=http://www.ams.org/bookstore-getitem/item=GSM-94 | publisher=American Mathematical Society | location=Providence, R.I. | series=Graduate Studies in Mathematics | isbn=978-0-8218-4678-0 | mr=2428237 | year=2008 | volume=94}}
• {{Citation | last1=Jantzen | first1=Jens Carsten | title=Moduln mit einem höchsten Gewicht | publisher=Springer-Verlag | location=Berlin, New York | series=Lecture Notes in Mathematics | isbn=978-3-540-09558-3 | doi=10.1007/BFb0069521 | mr=552943 | year=1979 | volume=750}}

• Spanish expeditions to the Pacific Northwest
• Spanish expulsion
• Spanish F3
• Spanish Federation Cup
• Spanish Fidelist Group of Cuba
• Spanish Fighting Bull
• Spanish-Filipino
• Spanish Filipino
• Spanish Filipinos
• Spanish-Filipinos
• Spanish film
• Spanish Films
• Spanish Fir
• Spanish flea
• Spanish Flea
• Spanish Florida
• Spanish Flower
• Spanish flower
• Spanish flu epidemic
• Spanish flu epidemic of 1918
• Spanish Flu Pandemic
• Spanish flu research
• Spanish Fly (album)
• Spanish Fly (Beavis and Butt-head Episode)
• Spanish fly (insect)