请输入您要查询的百科知识：

　

词条 Jaynes–Cummings–Hubbard model
释义

  1. History

  2. Properties

     Hamiltonian  Two-polariton bound states 

  3. Further reading

  4. See also

  5. References

The Jaynes-Cummings-Hubbard (JCH) model is a many-body quantum system modeling the quantum phase transition of light. As the name suggests, the Jayne-Cummings-Hubbard model is a variant on the Jaynes–Cummings model; a one-dimensional JCH model consists of a chain of N coupled single-mode cavities, each with a two-level atom. Unlike in the competing Bose-Hubbard model, Jayne-Cummings-Hubbard dynamics depend on photonic and atomic degrees of freedom and hence require strong-coupling theory for treatment.[1] One method for realizing an experimental model of the system uses circularly-linked superconducting qubits.[2]

History

The JCH model was originally proposed in June 2006 in the context of Mott transitions for strongly interacting photons in coupled cavity arrays.[3] A different interaction scheme was synchronically suggested, wherein four level atoms interacted with external fields, leading to polaritons with strongly correlated dynamics.[4]

Properties

Using mean-field theory to predict the phase diagram of the JCH model, the JCH model should exhibit Mott insulator and superfluid phases.[5]

Hamiltonian

The Hamiltonian of the JCH model is

():

where are Pauli operators for the two-level atom at the

n-th cavity. The is the tunneling rate between neighboring cavities, and is the vacuum Rabi frequency which characterizes to the photon-atom interaction strength. The cavity frequency is and atomic transition frequency is 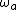. The cavities are treated as periodic, so that the cavity labelled by n = N+1 corresponds to the cavity n = 1.[3] Note that the model exhibits quantum tunneling; this is process is similar to the Josephson effect.[6][7]

Defining the photonic and atomic excitation number operators as 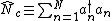and 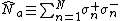, the total number of excitations a conserved quantity,

i.e., 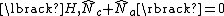.{{citation needed|date=November 2016}}

Two-polariton bound states

The JCH Hamiltonian supports two-polariton bound states when the photon-atom interaction is sufficiently strong. In particular, the two polaritons associated with the bound states exhibit a strong correlation such that they stay close to each other in position space.[8] This process is similar to the formation of a bound pair of repulsive bosonic atoms in an optical lattice.[9][10][11]

Further reading

  • D. F. Walls and G. J. Milburn (1995), Quantum Optics, Springer-Verlag.

See also

  • Bose-Hubbard model
  • Jaynes-Cummings model
  • Quantum phase transition

References

1. ^{{cite journal| title = Strong Coupling Theory for the Jaynes-Cummings-Hubbard Model|author1=Schmidt, S. |author2=Blatter, G.| journal = Phys. Rev. Lett.| volume = 103| issue = 8| pages = 086403|date=Aug 2009| doi = 10.1103/PhysRevLett.103.086403| url = http://link.aps.org/doi/10.1103/PhysRevLett.103.086403| publisher = American Physical Society|arxiv = 0905.3344 |bibcode = 2009PhRvL.103h6403S }}
2. ^{{cite journal|author1=A. Nunnenkamp |author2=Jens Koch |author3=S. M. Girvin | title = Synthetic gauge fields and homodyne transmission in Jaynes-Cummings lattices| journal = New Journal of Physics| year = 2011| volume = 13| pages = 095008| doi=10.1088/1367-2630/13/9/095008|arxiv = 1105.1817 |bibcode = 2011NJPh...13i5008N }}
3. ^1 {{cite journal|author1=D. G. Angelakis |author2=M. F. Santos |author3=S. Bose | title = Photon-blockade-induced Mott transitions and XY spin models in coupled cavity arrays| journal = Physical Review A| year = 2007| volume = 76| number = 03| pages = 1805(R)| doi=10.1103/physreva.76.031805|arxiv = quant-ph/0606159 |bibcode = 2007PhRvA..76c1805A }}
4. ^{{cite journal| author = M. J. Hartmann, F. G. S. L. Brandão and M. B. Plenio| title = Strongly interacting polaritons in coupled arrays of cavities| journal = Nature Physics| year = 2006| volume = 2| pages = 849| doi=10.1038/nphys462|arxiv = quant-ph/0606097 |bibcode = 2006NatPh...2..849H }}
5. ^{{cite journal|author1=A. D. Greentree |author2=C. Tahan |author3=J. H. Cole |author4=L. C. L. Hollenberg | title = Quantum phase transitions of light| journal = Nature Physics| year = 2006| volume = 2| pages = 856| doi=10.1038/nphys466|arxiv = cond-mat/0609050 |bibcode = 2006NatPh...2..856G }}
6. ^{{cite book| author = B. W. Petley| title = An Introduction to the Josephson Effects| publisher = Mills and Boon| location = London| year = 1971}}
7. ^{{cite book|author1=Antonio Barone |author2=Gianfranco Paternó | title = Physics and Applications of the Josephson Effect| publisher = Wiley| location = New York| year = 1982}}
8. ^{{cite journal| title = Two-polariton bound states in the Jaynes-Cummings-Hubbard model|author1=Max T. C. Wong |author2=C. K. Law | journal = Phys. Rev. A| volume = 83| issue = 5| pages = 055802|date=May 2011| doi = 10.1103/PhysRevA.83.055802| url = http://link.aps.org/doi/10.1103/PhysRevA.83.055802| publisher = American Physical Society|arxiv = 1101.1366 |bibcode = 2011PhRvA..83e5802W }}
9. ^{{cite journal|author1=K. Winkler |author2=G. Thalhammer |author3=F. Lang |author4=R. Grimm |author5=J. H. Denschlag |author6=A. J. Daley |author7=A. Kantian |author8=H. P. Buchler |author9=P. Zoller | title = Repulsively bound atom pairs in an optical lattice|journal = Nature| year = 2006| volume = 441| pages = 853| doi=10.1038/nature04918|arxiv = cond-mat/0605196 |bibcode = 2006Natur.441..853W | pmid=16778884}}
10. ^{{cite journal| title = Dimer of two bosons in a one-dimensional optical lattice| author = Javanainen, Juha and Odong, Otim and Sanders, Jerome C.| journal = Phys. Rev. A| volume = 81| issue = 4| pages = 043609|date=Apr 2010| doi = 10.1103/PhysRevA.81.043609| url = http://link.aps.org/doi/10.1103/PhysRevA.81.043609| publisher = American Physical Society|arxiv = 1004.5118 |bibcode = 2010PhRvA..81d3609J }}
11. ^{{cite journal|author1=M. Valiente |author2=D. Petrosyan | title = Two-particle states in the Hubbard model| journal = J. Phys. B: At. Mol. Opt. Phys.| year = 2008| volume = 41| pages = 161002| doi=10.1088/0953-4075/41/16/161002|bibcode = 2008JPhB...41p1002V |arxiv=0805.1812}}
{{DEFAULTSORT:Jaynes-Cummings-Hubbard model}}

1 : Quantum optics
随便看

　

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。

　

Copyright © 2023 OENC.NET All Rights Reserved
京ICP备2021023879号 更新时间：2024/11/11 4:26:55