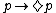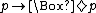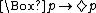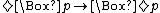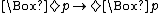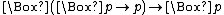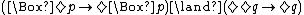“Sahlqvist formula”的意思、由来-开放百科全书

词条

Sahlqvist formula

释义

Definition
Examples of Sahlqvist formulas
Examples of non-Sahlqvist formulas
Kracht's theorem
References

In modal logic, Sahlqvist formulas are a certain kind of modal formula with remarkable properties. The Sahlqvist correspondence theorem states that every Sahlqvist formula is canonical, and corresponds to a first-order definable class of Kripke frames.

Sahlqvist's definition characterizes a decidable set of modal formulas with first-order correspondents. Since it is undecidable, by Chagrova's theorem, whether an arbitrary modal formula has a first-order correspondent, there are formulas with first-order frame conditions that are not Sahlqvist [Chagrova 1991] (see the examples below). Hence Sahlqvist formulas define only a (decidable) subset of modal formulas with first-order correspondents.

Definition

Sahlqvist formulas are built up from implications, where the consequent is positive and the antecedent is of a restricted form.

A boxed atom is a propositional atom preceded by a number (possibly 0) of boxes, i.e. a formula of the form 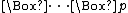(often abbreviated as 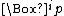for ).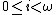
A Sahlqvist antecedent is a formula constructed using ∧, ∨, and from boxed atoms, and negative formulas (including the constants ⊥, ⊤).
A Sahlqvist implication is a formula A → B, where A is a Sahlqvist antecedent, and B is a positive formula.
A Sahlqvist formula is constructed from Sahlqvist implications using ∧ and (unrestricted), and using ∨ on formulas with no common variables.

Examples of Sahlqvist formulas

Its first-order corresponding formula is , and it defines all reflexive frames

Its first-order corresponding formula is , and it defines all symmetric frames

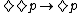or

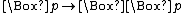
Its first-order corresponding formula is , and it defines all transitive frames

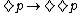or

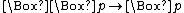
Its first-order corresponding formula is , and it defines all dense frames

Its first-order corresponding formula is , and it defines all right-unbounded frames (also called serial)

Its first-order corresponding formula is , and it is the Church-Rosser property.

Examples of non-Sahlqvist formulas

This is the McKinsey formula; it does not have a first-order frame condition.

The Löb axiom is not Sahlqvist; again, it does not have a first-order frame condition.

The conjunction of the McKinsey formula and the (4) axiom has a first-order frame condition (the conjunction of the transitivity property with the property ) but is not equivalent to any Sahlqvist formula.

Kracht's theorem

When a Sahlqvist formula is used as an axiom in a normal modal logic, the logic is guaranteed to be complete with respect to the elementary class of frames the axiom defines. This result comes from the Sahlqvist completeness theorem [Modal Logic, Blackburn et al., Theorem 4.42]. But there is also a converse theorem, namely a theorem that states which first-order conditions are the correspondents of Sahlqvist formulas. Kracht's theorem states that any Sahlqvist formula locally corresponds to a Kracht formula; and conversely, every Kracht formula is a local first-order correspondent of some Sahlqvist formula which can be effectively obtained from the Kracht formula [Modal Logic, Blackburn et al., Theorem 3.59].

References

L. A. Chagrova, 1991. An undecidable problem in correspondence theory. Journal of Symbolic Logic 56:1261–1272.
Marcus Kracht, 1993. How completeness and correspondence theory got married. In de Rijke, editor, Diamonds and Defaults, pages 175–214. Kluwer.
Henrik Sahlqvist, 1975. Correspondence and completeness in the first- and second-order semantics for modal logic. In Proceedings of the Third Scandinavian Logic Symposium. North-Holland, Amsterdam.

1 : Modal logic

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。