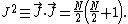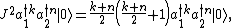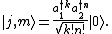“Jordan map”的意思、由来-开放百科全书

词条

Jordan map

释义

See also
References

In theoretical physics, the Jordan map, often also called the Jordan–Schwinger map is a map from matrices {{math|M_ij}} to bilinear expressions of quantum oscillators which expedites computation of representations of Lie Algebras occurring in physics. It was introduced by Pascual Jordan in 1935^[1] and was utilized by Julian Schwinger^[2] in 1952 to re-work out the theory of quantum angular momentum efficiently, given that map’s ease of organizing the (symmetric) representations of su(2) in Fock space.

The map utilizes several creation and annihilation operators

and 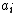of routine use in quantum field theories and many-body problems, each pair representing a quantum harmonic oscillator.

The commutation relations of creation and annihilation operators in a multiple-boson system are,

where 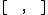is the commutator and is the Kronecker delta.

These operators change the eigenvalues of the number operator,

,

by one, as for multidimensional quantum harmonic oscillators.

The Jordan map from a set of matrices {{math|M_ij}} to Fock space bilinear operators {{math|M}},

is clearly a Lie Algebra isomorphism, i.e. the operators {{math|M}} satisfy the same commutation relations as the matrices {{math|M}}.

For example, the image of the Pauli matrices of SU(2) in this map,

for two-vector a^†s, and as satisfy the same commutation relations of SU(2) as well, and moreover, by reliance on the completeness relation for Pauli matrices,

This is the starting point of Schwinger’s treatment of the theory of quantum angular momentum, predicated on the action of these operators on Fock states built of arbitrary higher powers of such operators. For instance, acting on an (unnormalized) Fock eigenstate,

while

so that, for {{math| j{{=}}(k+n)/2, m{{=}}(k−n)/2}}, this is proportional to the eigenstate {{math|{{!}}j,m〉}}, ^[3]

Observe and .

Antisymmetric representations of Lie algebras can further be accommodated by use of the fermionic operators

and , as also suggested by Jordan. For fermions, the commutator is replaced by the anticommutator ,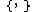

Therefore, exchanging disjoint (i.e. 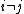) operators in a product of creation of annihilation operators will reverse the sign in fermion systems, but not in boson systems.

References

1. ^Jordan, Pascual (1935). "Der Zusammenhang der symmetrischen und linearen Gruppen und das Mehrkörperproblem", Zeitschrift für Physik 94, Issue 7-8, 531-535
2. ^Schwinger, J. (1952). "On Angular Momentum", Unpublished Report, Harvard University, Nuclear Development Associates, Inc., United States Department of Energy (through predecessor agency the Atomic Energy Commission), Report Number NYO-3071 (January 26, 1952).
3. ^Sakurai, J J and Napolitano, J J (2010), Modern Quantum Mechanics, Pearson {{isbn| 978-0805382914}}.

3 : Representation theory of Lie algebras|Mathematical physics|Theoretical physics

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。

See also

References