- See also
- Sources
Kellogg's theorem is a pair of related results in the mathematical study of the regularity of harmonic functions on sufficiently smooth domains by Oliver Dimon Kellogg.
In the first version, it states that, for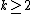 
, if the domain's boundary is of class 
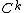and the k-th derivatives of the boundary are Dini continuous, then the harmonic functions are uniformly 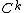as well. The second, more common version of the theorem states that for domains which are 
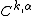, if the boundary data is of class 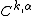, then so is the harmonic function itself.
Kellogg's method of proof analyzes the representation of harmonic functions provided by the Poisson kernel, applied to an interior tangent sphere.
In modern presentations, Kellogg's theorem is usually covered as a specific case of the boundary Schauder estimates for elliptic partial differential equations.
See also
- Schauder estimates
Sources
- {{Citation|last=Kellogg|first=Oliver Dimon|author-link=Oliver Dimon Kellogg|date=1931|title=On the derivatives of harmonic functions on the boundary|periodical=Transactions of the American Mathematical Society|volume=33|pages=486–510|url=http://www.ams.org/journals/tran/1931-033-02/S0002-9947-1931-1501602-2/home.html|doi=10.2307/1989419}}
- {{citation|first1=David|last=Gilbarg|authorlink1=David Gilbarg|first2=Neil|last2=Trudinger|authorlink2=Neil Trudinger|title=Elliptic Partial Differential Equations of Second Order|publisher=Springer|publication-place=New York|year=1983|isbn=3-540-41160-7}}
- Phillips' Ferry (Merced River)
- Phillips Field
- Phillip's Garden
- Phillips gelcaps
- Phillips Glacier
- Phillips Gold Medal
- Phillips Haymakers
- Phillip Shead
- Phillip Sheppard
- Phillips High School (Phillips, Wisconsin)
- Phillip Shiller
- Phillipshill wood
- Phillips Hill wood
- Phillips Hill Wood
- Phillipshill Wood
- Phillips Hill woods
- Phillips Hill Woods
- Phillipshill Woods
- Phillipshill woods
- Phillips House (disambiguation)
- Phillipsia lutea
- Phillipsia subpurpurea
- Phillipsiidae
- Phillip Simmonds
- Phillip Sims