“Key-independent optimality”的意思、由来-开放百科全书

词条

Key-independent optimality

释义

Definitions
Relationship with other bounds
References

Key-independent optimality is a property of some binary search tree data structures in computer science

proposed by John Iacono.^[1]

Suppose that key-value pairs are stored in a data

structure, and that the keys have no relation to their paired values.

A data structure has key-independent optimality if, when randomly assigning the keys, the expected performance of the data structure is within a constant factor of the optimal data structure. Key-independent optimality is related to dynamic optimality.

Definitions

There are many binary search tree algorithms that

can look up a sequence of

keys 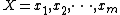, where each

is a number between and .

For each sequence , let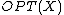

be the fastest binary search tree algorithm that looks up the elements in in order.

Let be one of the

possible

permutation of the sequence 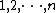, chosen at random,

where

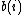is the th entry of .

Let .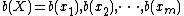

Iacono defined, for a sequence , that .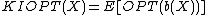

A data structure has key-independent optimality

if it can lookup the elements in in time

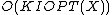Relationship with other bounds

Key-independent optimality has been proved to be asymptotically equivalent to

the

working set theorem.

Splay trees are known to have key-independent optimality.

References

1. ^{{cite web|title=John Iacono. Key independent optimality. Algorithmica, 42(1):3-10, 2005.|url=http://john2.poly.edu/papers/algo04/paper.pdf|deadurl=yes|archiveurl=https://web.archive.org/web/20100613054302/http://john2.poly.edu/papers/algo04/paper.pdf|archivedate=2010-06-13|df=}}

1 : Trees (data structures)

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。