“Kibble–Zurek mechanism”的意思、由来-开放百科全书

The Kibble–Zurek mechanism (KZM) describes the non-equilibrium dynamics and the formation of topological defects in a system which is driven through a continuous phase transition at finite rate. It is named after Tom W. B. Kibble, who pioneered the study of domain structure formation in the early universe,^[1]^[2] and Wojciech H. Zurek, who related the number of defects it creates to the critical exponents of the transition and to its rate - to how quickly the critical point is traversed.^[3]^[4]^[5]

Details

The mechanism exploits the critical slowing down in the neighbourhood of the critical point, this is, the divergence of the relaxation time of the system.

As the system approaches the critical point from the high symmetry phase, its dynamics becomes increasingly slow, and eventually ceases to be adiabatic.

Under a linear quench of the control parameter, this happens at the freeze-out time scale, when the relaxation time matches the time left for the system to reach the critical point. KZM predicts the typical size of the domains in the broken symmetry phase to be fixed by the value of the equilibrium correlation length at freeze-out time. The inverse of this length scale can be used as an estimate of the density of topological defects, and it obeys a power law in the quench rate. This prediction is universal, and the power exponent is given in terms of the critical exponents of the transition.

The KZM generally applies to spontaneous symmetry breaking scenarios where a global symmetry is broken.

For gauge symmetries defect formation can arise through the KZM and the flux trapping mechanism proposed by Hindmarsh and Rajantie.^[6]^[7]

In 2005, it was shown that KZM describes as well the dynamics through a quantum phase transition.^[8]^[9]^[10]^[11]

The mechanism also applies in the presence of inhomogeneities,^[12] ubiquitous in condensed matter experiments, to both classical,^[13]^[14]^[15] quantum phase transitions^[16]^[17] and even in optics.^[18]

Derivation of the defect density

Let us consider a system that undergoes a continuous phase transition at the critical value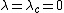

of a control parameter.

The theory of critical phenomena states that, as the control parameter is tuned closer and closer to its critical value, the correlation length and the relaxation time of the system tend to diverge as

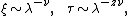
respectively. The KZM describes the nonadiabatic dynamics resulting from driving a high symmetry phase

to a broken symmetry phase at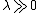

. If the control parameter varies linearly in time,

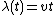, equating the time to the critical point to the relaxation time, we obtain the freeze out time

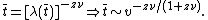
This time scale is often referred to as the freeze-out time. As the system approaches the critical point, it freezes as a result of the critical slowing down and falls out of equilibrium. Adiabaticity is lost

around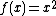

. Adiabaticity is restored in the broken symmetry phase after

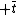. The correlation length at this time provides a length scale for coherent domains,

The size of the domains in the broken symmetry phase is set by

. The density of defects immediately follows, using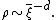

References

1. ^{{Cite journal |last = Kibble |first=T. W. B.|title=Topology of cosmic domains and strings|journal=J. Phys. A: Math. Gen.|volume=9|issue=8|pages=1387–1398 |date=1976|doi = 10.1088/0305-4470/9/8/029|bibcode = 1976JPhA....9.1387K }}
2. ^{{Cite journal |last = Kibble |first=T. W. B.|title=Some implications of a cosmological phase transition|journal=Phys. Rep.|volume=67|issue=1|pages=183–199 |date=1980|doi = 10.1016/0370-1573(80)90091-5 |bibcode = 1980PhR....67..183K }}
3. ^{{Cite journal |last = Zurek |first=W. H.|title=Cosmological experiments in superfluid helium?|journal=Nature|volume=317|issue=6037|pages=505–508|date=1985|doi = 10.1038/317505a0 |bibcode = 1985Natur.317..505Z }}
4. ^{{Cite journal |last = Zurek |first=W. H.|title=Cosmic Strings in Laboratory Superfluids and the Topological Remnants of Other Phase Transitions|journal= Acta Phys. Pol. B|volume=24|pages=1301|date=1993|url = http://th-www.if.uj.edu.pl/acta/vol24/abs/v24p1301.htm }}
5. ^{{Cite journal |last = Zurek |first=W. H.|title=Cosmological experiments in condensed matter systems|journal=Phys. Rep.|volume=276|issue=4|pages=177–221 |date=1996|doi = 10.1016/S0370-1573(96)00009-9 |arxiv = cond-mat/9607135 |bibcode = 1996PhR...276..177Z |citeseerx=10.1.1.242.1418}}
6. ^{{Cite journal |last=Hindmarsh |first=M. |last2=Rajantie |first2=A. |title=Defect Formation and Local Gauge Invariance |journal=Phys. Rev. Lett. |volume=85 |issue=22 |pages=4660–3 |date=2000 |doi=10.1103/PhysRevLett.85.4660 |arxiv=cond-mat/0007361 |bibcode=2000PhRvL..85.4660H |pmid=11082621 }}
7. ^{{Cite journal |last = Rajantie |first=A.|title=Formation of topological defects in gauge field theories|journal= Int. J. Mod. Phys. A|volume=17|issue=1|pages= 1–43|date=2002|doi = 10.1142/S0217751X02005426 |arxiv = hep-ph/0108159 |bibcode = 2002IJMPA..17....1R }}
8. ^{{Cite journal |last=Damski |first=B. |title=The Simplest Quantum Model Supporting the Kibble-Zurek Mechanism of Topological Defect Production: Landau-Zener Transitions from a New Perspective |journal=Phys. Rev. Lett. |volume=95 |issue=3 |pages=035701 |date=2005 |doi=10.1103/PhysRevLett.95.035701 |arxiv=cond-mat/0411004 |bibcode=2005PhRvL..95c5701D |pmid=16090756 }}
9. ^{{Cite journal |last=Zurek |first=W. H. |last2=Dorner |first2=U. |last3=Zoller |first3=P. |title=Dynamics of a Quantum Phase Transition |journal=Phys. Rev. Lett. |volume=95 |issue=10 |pages=105701 |date=2005 |doi=10.1103/PhysRevLett.95.105701 |pmid=16196941 |arxiv=cond-mat/0503511 |bibcode=2005PhRvL..95j5701Z }}
10. ^{{Cite journal |last=Dziarmaga |first=J. |title=Dynamics of a Quantum Phase Transition: Exact Solution of the Quantum Ising Model |journal=Phys. Rev. Lett. |volume=95 |issue=24 |pages=245701 |date=2005 |doi=10.1103/PhysRevLett.95.245701 |pmid=16384394 |arxiv=cond-mat/0509490 |bibcode=2005PhRvL..95x5701D }}
11. ^{{Cite journal |last=Polkovnikov |first=A. |title=Universal adiabatic dynamics in the vicinity of a quantum critical point |journal=Phys. Rev. B |volume=72 |issue=16 |pages=161201(R) |date=2005 |doi=10.1103/PhysRevB.72.161201 |arxiv=cond-mat/0312144 |bibcode=2005PhRvB..72p1201P }}
12. ^{{Cite journal |last = del Campo |first=A.|last2 = Kibble |first2=T. W. B.|last3 = Zurek |first3= W. H. |title = Causality and non-equilibrium second-order phase transitions in inhomogeneous systems |journal = J. Phys.: Condens. Matter |volume = 25|issue=40|pages = 404210|date = 2013|doi = 10.1088/0953-8984/25/40/404210|pmid=24025443|arxiv =1302.3648 |bibcode = 2013JPCM...25N4210D }}
13. ^{{Cite journal |last = Kibble |first=T. W. B. |last2 = Volovik |first2 = G. E.|title = On Phase Ordering Behind the Propagating Front of a Second-Order Transition |journal = JETP Lett. |volume = 65|issue=1 |pages = 102|date = 1997|doi = 10.1134/1.567332 |arxiv = cond-mat/9612075 |bibcode = 1997JETPL..65..102K }}
14. ^{{Cite journal |last=Zurek |first=W. H. |title=Causality in Condensates: Gray Solitons as Relics of BEC Formation |journal=Phys. Rev. Lett. |volume=102 |issue=10 |pages=105702 |date=2009 |doi=10.1103/PhysRevLett.102.105702 |arxiv=0902.3980 |bibcode=2009PhRvL.102j5702Z |pmid=19392126 }}
15. ^{{Cite journal |last=del Campo |first=A. |last2=De Chiara |first2=G. |last3=Morigi |first3=G. |last4=Plenio |first4=M. B. |last5=Retzker |first5=A. |title=Structural Defects in Ion Chains by Quenching the External Potential: The Inhomogeneous Kibble-Zurek Mechanism |journal=Phys. Rev. Lett. |volume=105 |issue=7 |pages=075701 |date=2010 |doi=10.1103/PhysRevLett.105.075701 |arxiv=1002.2524 |bibcode=2010PhRvL.105g5701D |pmid=20868058 }}
16. ^{{Cite journal |last = Zurek |first=W. H.|last2 =Dorner |first2= U.|title= Phase transition in space: how far does a symmetry bend before it breaks?|journal=Phil. Trans. R. Soc. A|volume= 366|issue=1877|pages= 2953–72|date=2008|doi = 10.1098/rsta.2008.0069|pmid=18534945|arxiv = 0807.3516 |bibcode = 2008RSPTA.366.2953Z }}
17. ^{{Cite journal |last = Dziarmaga |first=J.|last2 =Rams |first2= M. M.|title= Dynamics of an inhomogeneous quantum phase transition|journal=New J. Phys. |volume=12|issue=5|pages= 055007|date=2010|doi = 10.1088/1367-2630/12/5/055007 |arxiv = 0904.0115 |bibcode = 2010NJPh...12e5007D }}
18. ^{{Cite journal |last = Pal |first=V.|display-authors=etal|title= Observing Dissipative Topological Defects with Coupled Lasers|journal=Phys. Rev. Lett.|volume=119|issue=1|pages= 013902|date=2017|doi = 10.1103/PhysRevLett.119.013902|pmid=28731766|bibcode=2017PhRvL.119a3902P|arxiv=1611.01622}}
19. ^{{Cite journal |last = del Campo |first=A.|last2 = Zurek |first2= W. H. |title = Universality of phase transition dynamics: topological defects from symmetry breaking |journal = Int. J. Mod. Phys. A |volume = 29|issue=8|pages = 1430018|date = 2014|doi = 10.1142/S0217751X1430018X|arxiv=1310.1600|bibcode=2014IJMPA..2930018D}}