“Kinetic triangulation”的意思、由来-开放百科全书

A Kinetic Triangulation data structure is a kinetic data structure that maintains a triangulation of a set of moving points. Maintaining a kinetic triangulation is important for applications that involve motion planning, such as video games, virtual reality, dynamic simulations and robotics.

Choosing a triangulation scheme

The efficiency of a kinetic data structure is defined based on the ratio of the number of internal events to external events, thus good runtime bounds can sometimes be obtained by choosing to use a triangulation scheme that generates a small number of external events.

For simple affine motion of the points, the number of discrete changes to the convex hull is estimated by

,^[2] thus the number of changes to any triangulation is also lower bounded by

. Finding any triangulation scheme that has a near-quadratic bound on the number of discrete changes is an important open problem.

Delaunay triangulation

The Delaunay triangulation seems like a natural candidate, but a tight analysis of the number of discrete changes that will occur to the Delaunay triangulation (external events) is one of the hardest problems in computational geometry,^[4] and the best currently known upper bound is

There is a kinetic data structure that efficiently maintains the Delaunay triangulation of a set of moving points,^[1] in which the ratio of the total number of events to the number of external events is

Other triangulations

Kaplan et al. developed a randomized triangulation scheme that experiences an expected number of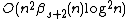

external events, where

is the maximum number of times each triple of points can become collinear,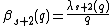

, and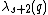

is the maximum length of a Davenport-Schinzel sequence of order s + 2 on n symbols.

Pseudo-triangulations

There is a kinetic data structure (due to Agarwal et al.) which maintains a pseudo-triangulation in

events total.^[2] All events are external and require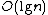

time to process.

References

1. ^Gerhard Albers, Leonidas J. Guibas, Joseph S. B. Mitchell, and Thomas Roos. Voronoi diagrams of moving points. Int. J. Comput. Geometry Appl., 8(3):365{380, 1998.
2. ^Pankaj K. Agarwal, Julien Basch, Leonidas J. Guibas, John Hershberger, and Li Zhang. Deformable free-space tilings for kinetic collision detection. I. J. Robotic Res., 21(3):179{198, 2002.
3. ^¹{{cite book | title=Davenport-Schinzel sequences and their geometric applications | publisher=, Cambridge University Press |author1=Sharir, M, |author2=Agarwal, P.K. | year=1995 | location=New York}}
4. ^¹{{cite web | url=http://www.cs.smith.edu/~orourke/TOPP/ | title=The Open Problems Project | accessdate=May 19, 2012 |author1=Demaine, E.D. |author2=Mitchell, J. S. B. |author3=O’Rourke, J. }}