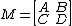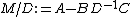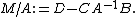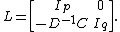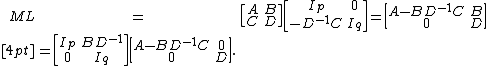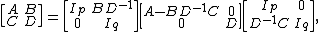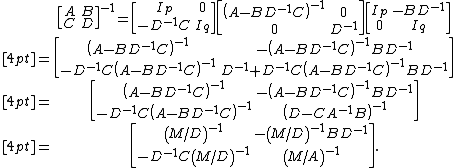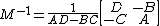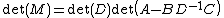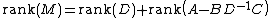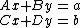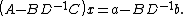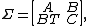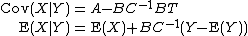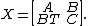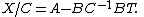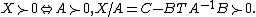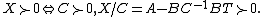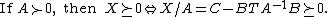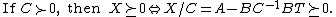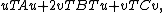- Background
- Properties
- Application to solving linear equations
- Applications to probability theory and statistics
- Schur complement condition for positive definiteness and positive semi-definiteness
- See also
- References
In linear algebra and the theory of matrices, the Schur complement of a block matrix is defined as follows.
Suppose A, B, C, D are respectively p × p, p × q, q × p, and q × q matrices, and D is invertible. Let
so that M is a (p + q) × (p + q) matrix.
Then the Schur complement of the block D of the matrix M is the p × p matrix defined by
and, if A is invertible, the Schur complement of the block A of the matrix M is the q × q matrix defined by
In the case that A or D is singular, substituting a generalized inverse for the inverses on M/A and M/D yields the generalized Schur complement.
The Schur complement is named after Issai Schur who used it to prove Schur's lemma, although it had been used previously.[1] Emilie Haynsworth was the first to call it the Schur complement.[2] The Schur complement is a key tool in the fields of numerical analysis, statistics and matrix analysis.
Background
The Schur complement arises as the result of performing a block Gaussian elimination by multiplying the matrix M from the right with a block lower triangular matrix
Here Ip denotes a p×p identity matrix. After multiplication with the matrix L the Schur complement appears in the upper p×p block. The product matrix is
This is analogous to an LDU decomposition. That is, we have shown that
and inverse of M thus may be expressed involving D−1 and the inverse of Schur's complement (if it exists) only as
Cf. matrix inversion lemma which illustrates relationships between the above and the equivalent derivation with the roles of A and D interchanged.
Properties
- If M is a positive-definite symmetric matrix, then so is the Schur complement of D in M.
- If p and q are both 1 (i.e., A, B, C and D are all scalars), we get the familiar formula for the inverse of a 2-by-2 matrix:
provided that AD − BC is non-zero.
- In general, if A is invertible, then
whenever this inverse exists.
- The determinant of M is also clearly seen to be given by
which generalizes the determinant formula for 2 × 2 matrices.
- (Guttman rank additivity formula) The rank of M is given by
- (Haynsworth inertia additivity formula) The inertia of the block matrix M is equal to the inertia of A plus the inertia of M/A.
Application to solving linear equations
The Schur complement arises naturally in solving a system of linear equations such as
where x, a are p-dimensional column vectors, y, b are q-dimensional column vectors, and A, B, C, D are as above. Multiplying the bottom equation by 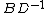 and then subtracting from the top equation one obtains
and then subtracting from the top equation one obtains
Thus if one can invert D as well as the Schur complement of D, one can solve for x, and
then by using the equation 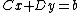 one can solve for y. This reduces the problem of inverting a
one can solve for y. This reduces the problem of inverting a 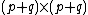 matrix to that of inverting a p × p matrix and a q × q matrix. In practice, one needs D to be well-conditioned in order for this algorithm to be numerically accurate.
matrix to that of inverting a p × p matrix and a q × q matrix. In practice, one needs D to be well-conditioned in order for this algorithm to be numerically accurate.
In electrical engineering this is often referred to as node elimination or Kron reduction.
Applications to probability theory and statistics
Suppose the random column vectors X, Y live in Rn and Rm respectively, and the vector (X, Y) in Rn + m has a multivariate normal distribution whose covariance is the symmetric positive-definite matrix
where  is the covariance matrix of X,
is the covariance matrix of X, 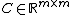 is the covariance matrix of Y and
is the covariance matrix of Y and 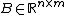 is the covariance matrix between X and Y.
is the covariance matrix between X and Y.
Then the conditional covariance of X given Y is the Schur complement of C in  [3]:
[3]:
If we take the matrix  above to be, not a covariance of a random vector, but a sample covariance, then it may have a Wishart distribution. In that case, the Schur complement of C in
above to be, not a covariance of a random vector, but a sample covariance, then it may have a Wishart distribution. In that case, the Schur complement of C in  also has a Wishart distribution.{{Citation needed|date=January 2014}}
also has a Wishart distribution.{{Citation needed|date=January 2014}}
Schur complement condition for positive definiteness and positive semi-definiteness
Let X be a symmetric matrix given by
Let X/A be the Schur complement of A in X; i.e.,
and X/C be the Schur complement of C in X; i.e.,
Then
- X is positive definite if and only if A and X/A are both positive definite:
- X is positive definite if and only if C and X/C are both positive definite:
- If A is positive definite, then X is positive semi-definite if and only if X/A is positive semi-definite:
- If C is positive definite, then X is positive semi-definite if and only if X/C is positive semi-definite:
The first and third statements can be derived[4] by considering the minimizer of the quantity
as a function of v (for fixed u).
Furthermore, since
and similarly for positive semi-definite matrices, the second (respectively fourth) statement is immediate from the first (resp. third) statement.
There is also a sufficient and necessary condition for the positive semi-definiteness of X in terms of a generalized Schur complement.[1] Precisely,
-
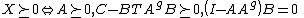 and
and -
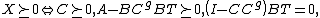
where 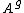 denotes the generalized inverse of
denotes the generalized inverse of  .
.
See also
- Woodbury matrix identity
- Quasi-Newton method
- Haynsworth inertia additivity formula
- Gaussian process
- Total least squares
References
2. ^Haynsworth, E. V., "On the Schur Complement", Basel Mathematical Notes, #BNB 20, 17 pages, June 1968.
3. ^{{cite book |title=Mathematical theory of probability and statistics |first=Richard |last=von Mises |year=1964|publisher=Academic Press| chapter=Chapter VIII.9.3|isbn=978-1483255385}}
4. ^Boyd, S. and Vandenberghe, L. (2004), "Convex Optimization", Cambridge University Press (Appendix A.5.5)
- 4th SA Infantry Regiment
- 4th San Diego Film Awards
- 4th Saturn Awards
- 4th sector of Marseille
- 4th shore
- 4th Siberian Army Corps
- 4th Siberian Rifle Division (Russian Empire)
- 4th Squadron (JASDF)
- 4th Staffordshire Battery, Royal Field Artillery
- 4th State Duma
- 4th State Duma of the Russian Federation
- 4th Streamy Awards
- 4th Street Corridor, Long Beach, California
- 4th Street (song)
- 4th Street (Washington, D.C.)
- 4th Sussex Artillery Volunteers
- 4th Sussex Battery, Royal Field Artillery
- 4th Tactical Reconnaissance Squadron
- 4th Tank Regiment
- 4th Tank Regiment (Japan)
- 4th Temple
- 4th (Torquay) Devonshire Artillery Volunteer Corps
- 4th Tower Hamlets Rifle Volunteer Corps
- 4th (Town of Aberdeen) Aberdeenshire Artillery Volunteer Corps
- 4th Troop, Bombay Horse Artillery