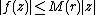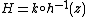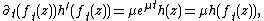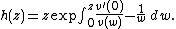“Koenigs function”的意思、由来-开放百科全书

词条

Koenigs function

释义

Existence and uniqueness of Koenigs function
Proof
Koenigs function of a semigroup
Structure of univalent semigroups
Notes
References

In mathematics, the Koenigs function is a function arising in complex analysis and dynamical systems. Introduced in 1884 by the French mathematician Gabriel Koenigs, it gives a canonical representation as dilations of a univalent holomorphic mapping, or a semigroup of mappings, of the unit disk in the complex numbers into itself.

Existence and uniqueness of Koenigs function

Let D be the unit disk in the complex numbers. Let {{mvar|f}} be a holomorphic function mapping D into itself, fixing the point 0, with {{mvar|f}} not identically 0 and {{mvar|f}} not an automorphism of D, i.e. a Möbius transformation defined by a matrix in SU(1,1).

By the Denjoy-Wolff theorem, {{mvar|f}} leaves invariant each disk |z | < r and the iterates of {{mvar|f}} converge uniformly on compacta to 0: in fact for 0 < {{mvar|r}} < 1,

for |z | ≤ r with M(r ) < 1. Moreover {{mvar|f}} '(0) = {{mvar|λ}} with 0 < |{{mvar|λ}}| < 1.

{{harvtxt|Koenigs|1884}} proved that there is a unique holomorphic function h defined on D, called the Koenigs function,

such that {{mvar|h}}(0) = 0, {{mvar|h}} '(0) = 1 and Schröder's equation is satisfied,

The function h is the uniform limit on compacta of the normalized iterates, .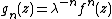

Moreover, if {{mvar|f}} is univalent, so is {{mvar|h}}.^[1]^[2]

As a consequence, when {{mvar|f}} (and hence {{mvar|h}}) are univalent, {{mvar|D}} can be identified with the open domain {{math|U {{=}} h(D)}}. Under this conformal identification, the mapping {{mvar|f}} becomes multiplication by {{mvar|λ}}, a dilation on {{mvar|U}}.

Proof

Uniqueness. If {{mvar|k}} is another solution then, by analyticity, it suffices to show that k = h near 0. Let

near 0. Thus H(0) =0, H'(0)=1 and, for |z | small,

Substituting into the power series for {{mvar|H}}, it follows that {{math|H(z) {{=}} z}} near 0. Hence {{math|h {{=}} k}} near 0.

Existence. If then by the Schwarz lemma

On the other hand,

Hence g_n converges uniformly for |z| ≤ r by the Weierstrass M-test since

Univalence. By Hurwitz's theorem, since each gⁿ is univalent and normalized, i.e. fixes 0 and has derivative 1 there , their limit {{mvar|h}} is also univalent.

Koenigs function of a semigroup

Let {{math|f_t (z)}} be a semigroup of holomorphic univalent mappings of {{mvar|D}} into itself fixing 0 defined

for {{math| t ∈ [0, ∞)}} such that

is not an automorphism for {{mvar|s}} > 0
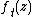is jointly continuous in {{mvar|t}} and {{mvar|z}}

Each {{math|f_s}} with {{mvar|s}} > 0 has the same Koenigs function, cf. iterated function. In fact, if h is the Koenigs function of

{{math|f {{=}} f₁}}, then {{math|h(f_s(z))}} satisfies Schroeder's equation and hence is proportion to h.

Taking derivatives gives

Hence {{mvar|h}} is the Koenigs function of {{math|f_s}}.

Structure of univalent semigroups

On the domain {{math|U {{=}} h(D)}}, the maps {{math|f_s}} become multiplication by 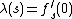, a continuous semigroup.

So 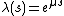where {{mvar|μ}} is a uniquely determined solution of {{math|e ^μ {{=}} λ}} with Re{{mvar|μ}} < 0. It follows that the semigroup is differentiable at 0. Let

a holomorphic function on {{mvar|D}} with v(0) = 0 and {{math|v(0)}} = {{mvar|μ}}.

Then

so that

and

the flow equation for a vector field.

Restricting to the case with 0 < λ < 1, the h(D) must be starlike so that

Since the same result holds for the reciprocal,

so that {{math|v(z)}} satisfies the conditions of {{harvtxt|Berkson|Porta|1978}}

Conversely, reversing the above steps, any holomorphic vector field {{math|v(z)}} satisfying these conditions is associated to a semigroup {{math|f_t}}, with

Notes

1. ^{{harvnb|Carleson|Gamelin|1993|pp=28–32}}
2. ^{{harvnb|Shapiro|1993|pp=90–93}}

References

{{citation|last=Berkson|first=E.|last2= Porta|first2= H.|title=Semigroups of analytic functions and composition operators|journal=

Michigan Math. J.|volume= 25|year= 1978|pages= 101–115|doi=10.1307/mmj/1029002009}}

{{citation|last=Carleson|first=L.|last2= Gamelin|first2= T. D. W.|title=Complex dynamics|series=

Universitext: Tracts in Mathematics|publisher= Springer-Verlag|year=1993|isbn=0-387-97942-5}}

{{citation|last2=Shoikhet|first2=D.|title=Linearization Models for Complex Dynamical Systems: Topics in Univalent Functions, Functional Equations and Semigroup Theory|volume=208|series= Operator Theory: Advances and Applications|first=M.|last= Elin|publisher=Springer|year= 2010|isbn= 978-3034605083}}
{{citation|first=G.P.X.|last=Koenigs|title=Recherches sur les intégrales de certaines équations fonctionnelles|journal=Ann. Sci. Ecole Norm. Sup.|volume= 1|year=1884|pages= 2–41}}
{{cite book |title=Functional equations in a single variable |last=Kuczma |first=Marek|authorlink=Marek Kuczma|series=Monografie Matematyczne |year=1968 |publisher=PWN – Polish Scientific Publishers |location=Warszawa}} ASIN: B0006BTAC2
{{citation|last=Shapiro|first=J. H.|title=Composition operators and classical function theory|series=Universitext: Tracts in Mathematics|publisher= Springer-Verlag|year= 1993|isbn=0-387-94067-7}}
{{citation|last=Shoikhet|first=D.|title=Semigroups in geometrical function theory|publisher= Kluwer Academic Publishers|year= 2001|isbn=

0-7923-7111-9 }}

3 : Complex analysis|Dynamical systems|Types of functions

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。