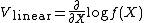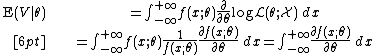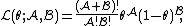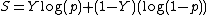“Score (statistics)”的意思、由来-开放百科全书

词条

Score (statistics)

释义

Definition
Properties
Mean Variance
Examples
Bernoulli process Binary outcome model
Applications
Scoring algorithm Score test
See also
Notes
References

In statistics, the score, score function, efficient score{{sfn|Cox|Hinkley|1974|p=107}} or informant^[1] indicates how sensitive a likelihood function is to its parameter . Explicitly, the score for

is the gradient of the log-likelihood with respect to .

The score plays an important role in several aspects of inference. For example:

in formulating a test statistic for a locally most powerful test;{{sfn|Cox|Hinkley|1974|p=113}}
in approximating the error in a maximum likelihood estimate;{{sfn|Cox|Hinkley|1974|p=295}}
in demonstrating the asymptotic sufficiency of a maximum likelihood estimate;{{sfn|Cox|Hinkley|1974|p=295}}
in the formulation of confidence intervals;{{sfn|Cox|Hinkley|1974|p=222–3}}
in demonstrations of the Cramér–Rao inequality.{{sfn|Cox|Hinkley|1974|p=254}}

The score function also plays an important role in computational statistics, as it can play a part in the computation of

maximum likelihood estimates.

Definition

The score is the gradient (the vector of partial derivatives), with respect to some parameter , of the logarithm (commonly the natural logarithm) of the likelihood function (the log-likelihood). If the observation is and its likelihood is , then the score can be found through the chain rule:

Thus the score indicates the sensitivity of (its derivative normalized by its value). Note that is a function of and the observation , so that, in general, it is not a statistic. However, in certain applications, such as the score test, the score is evaluated at a specific value of (such as a null-hypothesis value, or at the maximum likelihood estimate of ), in which case the result is a statistic.

In older literature, the term "linear score" may be used to refer to the score with respect to infinitesimal translation of a given density. This convention arises from a time when the primary parameter of interest was the mean or median of a distribution. In this case, the likelihood of an observation is given by a density of the form . The "linear score" is then defined as

Properties

Mean

Under some regularity conditions, the expected value of with respect to the observation , given the true parameter , written , is zero. To see this rewrite the likelihood function as a probability density function . Then:

If certain differentiability conditions are met (see Leibniz integral rule), the integral may be rewritten as

It is worth restating the above result in words: the expected value of the score is zero. Thus, if one were to repeatedly sample from some distribution, and repeatedly calculate the score, then the mean value of the scores would tend to zero as the number of repeat samples approached infinity.

Variance

The variance of the score is known as the Fisher information and is written . Because the expectation of the score is zero, this may be written as

Note that the Fisher information, as defined above, is not a function of any particular observation, as the random variable has been averaged out. This concept of information is useful when comparing two methods of observation of some random process.

Examples

Bernoulli process

Consider observing the first n trials of a Bernoulli process, and seeing that A of them are successes and the remaining B are failures, where the probability of success is θ.

Then the likelihood is

so the score V is

We can now verify that the expectation of the score is zero. Noting that the expectation of A is nθ and the expectation of B is n(1 − θ) [recall that A and B are random variables], we can see that the expectation of V is

We can also check the variance of . We know that A + B = n (so B = n − A) and the variance of A is nθ(1 − θ) so the variance of V is

Binary outcome model

For models with binary outcomes (Y = 1 or 0), the model can be scored with the logarithm of predictions

where p is the probability in the model to be estimated and S is the score.^[2]

Applications

Scoring algorithm

The scoring algorithm is an iterative method for numerically determining the maximum likelihood estimator.

Score test

Notes

1. ^{{SpringerEOM| title=Informant |id=i/i051030 |first=N.N. |last=Chentsov}}
2. ^{{cite journal |last=Steyerberg |first=E. W. |last2=Vickers |first2=A. J. |last3=Cook |first3=N. R. |last4=Gerds |first4=T. |last5=Gonen |first5=M. |last6=Obuchowski |first6=N. |last7=Pencina |first7=M. J. |last8=Kattan |first8=M. W. |year=2010 |title=Assessing the performance of prediction models. A framework for traditional and novel measures |journal=Epidemiology |volume=21 |issue=1 |pages=128–138 |doi=10.1097/EDE.0b013e3181c30fb2 |pmc=3575184 }}

References

{{cite book |last=Cox |first=D. R. |last2=Hinkley |first2=D. V. |year=1974 |title=Theoretical Statistics |location= |publisher=Chapman & Hall |isbn=0-412-12420-3 |ref=harv }}
{{cite book

| last = Schervish
| first = Mark J.
| title = Theory of Statistics
| publisher =Springer
| date =1995
| location =New York
| pages = Section 2.3.1
| isbn = 0-387-94546-6
| nopp = true}}

1 : Maximum likelihood estimation

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。