“Kummer's theorem”的意思、由来-开放百科全书

词条

Kummer's theorem

释义

Statement
Multinomial coefficient generalization
See also
References

In mathematics, Kummer's theorem for binomial coefficients gives the p-adic valuation of a binomial coefficient, i.e., the exponent of the highest power of a prime number p dividing this binomial coefficient. The theorem is named after Ernst Kummer, who proved it in the paper {{harvtxt|Kummer|1852}}.

Statement

Kummer's theorem states that for given integers n ≥ m ≥ 0 and a prime number p, the p-adic valuation 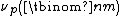is equal to the number of carries when m is added to n − m in base p.

It can be proved by writing 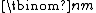as 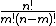and using Legendre's formula.

Multinomial coefficient generalization

Kummer's theorem may be generalized to multinomial coefficients 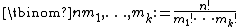as follows: Write the base- expansion of an integer as 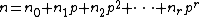, and define 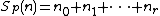to be the sum of the base- digits. Then

References

{{cite journal

|last=Kummer
|first=Ernst
|title=Über die Ergänzungssätze zu den allgemeinen Reciprocitätsgesetzen
|journal=Journal für die reine und angewandte Mathematik
|year=1852
|volume=44
|pages=93–146
|doi=10.1515/crll.1852.44.93}}

{{PlanetMath|urlname=KummersTheorem|title=Kummer's theorem}}

1 : Theorems in number theory

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。

Statement

Multinomial coefficient generalization

See also

References