“Lehmer's totient problem”的意思、由来-开放百科全书

词条

Lehmer's totient problem

释义

Properties
References
External links

{{for|Lehmer's Mahler measure problem|Lehmer's conjecture}}{{unsolved|mathematics|Can the totient function of a composite number

divide

?}}

In mathematics, Lehmer's totient problem asks whether there is any composite number n such that Euler's totient function φ(n) divides n − 1. This is an unsolved problem.

For every prime number n, we have φ(n) = n − 1 and so in particular φ(n) divides n − 1. D. H. Lehmer conjectured in 1932 that there are no composite numbers with this latter property.^[1]

Properties

Lehmer showed that if any composite solution n exists, it must be odd, square-free, and divisible by at least seven distinct primes (i.e. ω(n) ≥ 7). Such a number must also be a Carmichael number.
In 1980 Cohen and Hagis proved that, for any solution n to the problem, n > 10²⁰ and ω(n) ≥ 14.^[2]
In 1988 Hagis showed that if 3 divides any solution n then n > 10^1937042 and ω(n) ≥ 298848.^[3]
The number of solutions to the problem less than X is 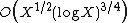.^[4]
In 2017, Shen lixing, a Chinese amateur, wrote two C programs and found 21568 Carmichael numbers (max prime factor is 241921) with ω(n) = 14 and found 87 Carmichael numbers with ω(n) = 15 below 10²⁶. None of them is a solution to this problem. According to a previous result from Richard Pinch, http://www.chalcedon.demon.co.uk/rgep/cartable.html, we can say, "n" > 10²⁶. In the web, he misprint 21568 in 10²⁷ column.

References

1. ^Lehmer (1932)
2. ^Sándor et al (2006) p.23
3. ^Guy (2004) p.142
4. ^Sándor et al (2006) p.24

{{cite journal | zbl=0436.10002 | last1=Cohen | first1=Graeme L. | last2=Hagis | first2=Peter, jun. | title=On the number of prime factors of n if φ(n) divides n−1 | journal=Nieuw Arch. Wiskd., III. Ser. | volume=28 | pages=177–185 | year=1980 | issn=0028-9825 }}
{{cite book |last=Guy | first=Richard K. | authorlink=Richard K. Guy | title=Unsolved problems in number theory | publisher=Springer-Verlag |edition=3rd | year=2004 |isbn=0-387-20860-7 | zbl=1058.11001 | at=B37}}
{{cite journal | zbl=0668.10006 | last=Hagis | first=Peter, jun. | title=On the equation M⋅φ(n)=n−1 | journal=Nieuw Arch. Wiskd., IV. Ser. | volume=6 | number=3 | pages=255–261 | year=1988 | issn=0028-9825 }}
{{cite journal | last=Lehmer | first=D. H. | authorlink=Derrick Henry Lehmer | title=On Euler's totient function | journal=Bulletin of the American Mathematical Society | volume=38 | pages=745–751 | year=1932 | issn=0002-9904 | zbl=0005.34302 | doi=10.1090/s0002-9904-1932-05521-5}}
{{cite book | last1=Ribenboim | first1=Paulo | authorlink=Paulo Ribenboim | edition=3rd | title=The New Book of Prime Number Records | publisher=Springer-Verlag | location=New York | year=1996 | isbn=0-387-94457-5 | zbl=0856.11001 }}
{{cite book | editor1-last=Sándor | editor1-first=József | editor2-last=Mitrinović | editor2-first=Dragoslav S. | editor3-last=Crstici | editor3-first=Borislav | title=Handbook of number theory I | location=Dordrecht | publisher=Springer-Verlag | year=2006 | isbn=1-4020-4215-9 | zbl=1151.11300 }}
{{cite journal | zbl=1240.11005| mr = 2894552 |last1=Burcsi | first1=Péter | last2=Czirbusz | first2=Sándor | last3=Farkas | first3=Gábor | title=Computational investigation of Lehmer's totient problem | journal=Ann. Univ. Sci. Budap. Rolando Eötvös, Sect. Comput. | volume=35 | pages=43–49 | year=2011 | issn=0138-9491 }}

External links

{{MathWorld | title=Lehmer's Totient Problem | id=LehmersTotientProblem }}

2 : Conjectures|Multiplicative functions

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。