“Self-adjoint”的意思、由来-开放百科全书

词条

Self-adjoint

释义

See also
References

In mathematics, an element x of a *-algebra is self-adjoint if .

A collection C of elements of a star-algebra is self-adjoint if it is closed under the involution operation. For example, if 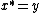then since in a star-algebra, the set {x,y} is a self-adjoint set even though x and y need not be self-adjoint elements.

In functional analysis, a linear operator A on a Hilbert space is called self-adjoint if it is equal to its own adjoint A{{sup|∗}} and that the domain of A is the same as that of A{{sup|∗}}. See self-adjoint operator for a detailed discussion. If the Hilbert space is finite-dimensional and an orthonormal basis has been chosen, then the operator A is self-adjoint if and only if the matrix describing A with respect to this basis is Hermitian, i.e. if it is equal to its own conjugate transpose. Hermitian matrices are also called self-adjoint.

In a dagger category, a morphism is called self-adjoint if 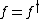; this is possible only for an endomorphism .

References

{{cite book |authorlink=Michael C. Reed |first=M. |last=Reed |authorlink2=Barry Simon |first2=B. |last2=Simon |title=Methods of Mathematical Physics |others=Vol 2 |publisher=Academic Press |year=1972 |isbn= }}
{{cite book |authorlink=Gerald Teschl |first=G. |last=Teschl |title=Mathematical Methods in Quantum Mechanics; With Applications to Schrödinger Operators |publisher=American Mathematical Society |location=Providence |year=2009 |url=http://www.mat.univie.ac.at/~gerald/ftp/book-schroe/ }}

2 : Abstract algebra|Linear algebra

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。

See also

References