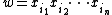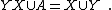“Monoid factorisation”的意思、由来-开放百科全书

词条

Monoid factorisation

释义

Chen–Fox–Lyndon theorem
Bisection
Schützenberger theorem
References

In mathematics, a factorisation of a free monoid is a sequence of subsets of words with the property that every word in the free monoid can be written as a concatenation of elements drawn from the subsets. The Chen–Fox–Lyndon theorem states that the Lyndon words furnish a factorisation. The Schützenberger theorem relates the definition in terms of a multiplicative property to an additive property.

Let A^* be the free monoid on an alphabet A. Let X_i be a sequence of subsets of A^* indexed by a totally ordered index set I. A factorisation of a word w in A^* is an expression

with 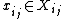and .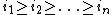

Chen–Fox–Lyndon theorem

A Lyndon word over a totally ordered alphabet A is a word which is lexicographically less than all its rotations.^[1] The Chen–Fox–Lyndon theorem states that every string may be formed in a unique way by concatenating a non-increasing sequence of Lyndon words. Hence taking X_l to be the singleton set {l} for each Lyndon word l, with the index set L of Lyndon words ordered lexicographically, we obtain a factorisation of A^*.^[2] Such a factorisation can be found in linear time.^[3]

Bisection

A bisection of a free monoid is a factorisation with just two classes X₀, X₁.^[4]

Examples:

A = {a,b}, X₀ = {a^*b}, X₁ = {a}.

If X, Y are disjoint sets of non-empty words, then (X,Y) is a bisection of A* if and only if^[5]

As a consequence, for any partition P , Q of A⁺ there is a unique bisection (X,Y) with X a subset of P and Y a subset of Q.^[6]

Schützenberger theorem

This theorem states that a sequence X_i of subsets of A^* forms a factorisation if and only if two of the following three statements holds:

Every element of A has at least one expression in the required form;
Every element of A has at most one expression in the required form;
Each conjugate class C meets just one of the monoids M_i = X_i and the elements of C in M_i are conjugate in M_i.^[7]

References

1. ^Lothaire (1997) p.64
2. ^Lothaire (1997) p.67
3. ^{{cite journal | last = Duval | first = Jean-Pierre | doi = 10.1016/0196-6774(83)90017-2 | issue = 4 | journal = Journal of Algorithms | pages = 363–381 | title = Factorizing words over an ordered alphabet | volume = 4 | year = 1983}}.
4. ^Lothaire (1997) p.68
5. ^Lothaire (1997) p.69
6. ^Lothaire (1997) p.71
7. ^Lothaire (1997) p.92

{{Citation | last=Lothaire | first=M. | authorlink=M. Lothaire | others=Perrin, D.; Reutenauer, C.; Berstel, J.; Pin, J. E.; Pirillo, G.; Foata, D.; Sakarovitch, J.; Simon, I.; Schützenberger, M. P.; Choffrut, C.; Cori, R.; Lyndon, Roger; Rota, Gian-Carlo. Foreword by Roger Lyndon | title=Combinatorics on words | edition=2nd | series=Encyclopedia of Mathematics and Its Applications | volume=17 | publisher=Cambridge University Press | year=1997 | isbn=0-521-59924-5 | zbl=0874.20040 }}

1 : Formal languages

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。