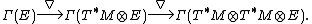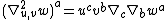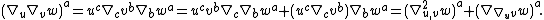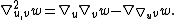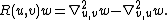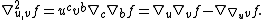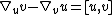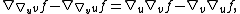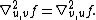“Second covariant derivative”的意思、由来-开放百科全书

词条

Second covariant derivative

释义

Definition
Notes

In the math branches of differential geometry and vector calculus, the second covariant derivative, or the second order covariant derivative, of a vector field is the derivative of its derivative with respect to another two tangent vector fields.

Definition

Formally, given a (pseudo)-Riemannian manifold (M, g) associated with a vector bundle E → M, let ∇ denote the Levi-Civita connection given by the metric g, and denote by Γ(E) the space of the smooth sections of the total space E. Denote by T^*M the cotangent bundle of M. Then the second covariant derivative can be defined as the composition of the two ∇s as follows: ^[1]

For example, given vector fields u, v, w, a second covariant derivative can be written as

by using abstract index notation. It is also straightforward to verify that

Thus

When the torsion tensor is zero, so that 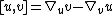, we may use this fact to write Riemann curvature tensor as ^[2]

Similarly, one may also obtain the second covariant derivative of a function f as

Again, for the torsion-free Levi-Civita connection, and for any vector fields u and v, when we feed the function f into both sides of

we find

.

This can be rewritten as

so we have

That is, the value of the second covariant derivative of a function is independent on the order of taking derivatives.

Notes

1. ^{{cite web|last1=Parker|first1=Thomas H.|title=Geometry Primer|url=http://www.math.msu.edu/~parker/ga/geometryprimer.pdf|accessdate=2 January 2015}}, pp. 7
2. ^{{cite web|author=Jean Gallier and Dan Guralnik|title=Chapter 13: Curvature in Riemannian Manifolds|url=http://www.cis.upenn.edu/~cis610/diffgeom5.pdf|accessdate=2 January 2015}}

2 : Tensors in general relativity|Riemannian geometry

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。