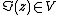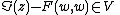请输入您要查询的百科知识：

　

词条 Siegel domain
释义

  1. Definitions

  2. Bounded homogeneous domains

  3. j-algebras

  4. References

In mathematics, a Siegel domain or Piatetski-Shapiro domain is a special open subset of complex affine space generalizing the Siegel upper half plane studied by {{harvs|txt|authorlink=Carl Ludwig Siegel|last=Siegel|year=1939}}. They were introduced by {{harvs|txt|authorlink=Ilya Piatetski-Shapiro|last=Piatetski-Shapiro|year1=1959|year2=1969}} in his study of bounded homogeneous domains.

Definitions

A Siegel domain of the first kind (or first type, or genus 1) is the open subset of Cm of elements z such that

where V is an open convex cone in Rm. These are special cases of tube domains. An example is the Siegel upper half plane, where V⊂Rk(k + 1)/2 is the cone of positive definite quadratic forms in Rk and m = k(k + 1)/2.

A Siegel domain of the second kind (or second type, or genus 2), also called a Piatetski-Shapiro domain, is the open subset of Cm×Cn of elements (z,w) such that

where V is an open convex cone in Rm and F is a V-valued Hermitian form on Cn.

If n = 0 this is a Siegel domain of the first kind.

A Siegel domain of the third kind (or third type, or genus 3) is the open subset of Cm×Cn×Ck of elements (z,w,t) such that

and t lies in some bounded region

where V is an open convex cone in Rm and Lt is a V-valued semi-Hermitian form on Cn.

Bounded homogeneous domains

A bounded domain is an open connected bounded subset of a complex affine space. It is called homogeneous if its group of automorphisms acts transitively, and is called symmetric if for every point there is an automorphism acting as –1 on the tangent space. Bounded symmetric domains are homogeneous.

Élie Cartan classified the homogeneous bounded domains in dimension at most 3 (up to isomorphism), showing that they are all Hermitian symmetric spaces. There is 1 in dimension 1 (the unit ball), two in dimension 2 (the product of two 1-dimensional complex balls or a 2-dimensional complex ball). He asked whether all bounded homogeneous domains are symmetric. {{harvs|txt|last=Piatetski-Shapiro|year1=1959|year2=1959b}} answered Cartan's question by finding a Siegel domain of type 2 in 4 dimensions that is homogeneous and biholomorphic to a bounded domain but not symmetric. In dimensions at least 7 there are infinite families of homogeneous bounded domains that are not symmetric.

{{harvs|txt| last1=Vinberg | first1=È. B. | last2=Gindikin | first2=S. G. | last3=Piatetski-Shapiro | first3=I. I. | year=1963 }} showed that every bounded homogeneous domain is biholomorphic to a Siegel domain of type 1 or 2.{{harvs|txt | last1=Kaup | first1=Wilhelm | last2=Matsushima | first2=Yozô | last3=Ochiai | first3=Takushiro |year=1970 }} described the isomorphisms of Siegel domains of types 1 and 2 and the Lie algebra of automorphisms of a Siegel domain. In particular two Siegel domains are isomorphic if and only if they are isomorphic by an affine transformation.

j-algebras

Suppose that G is the Lie algebra of a transitive connected group of analytic automorphisms of a bounded homogeneous domain X, and let K be the subalgebra fixing a point x. Then the almost complex structure j on X induces a vector space endomorphism j of G such that

  • j2=–1 on G/K
  • [x,y] + j[jx,y] + j[x,jy] – [jx,jy] = 0 in G/K; this follows from the fact that the almost complex structure of X is integrable
  • There is a linear form ω on G such that ω[jx,jy]=ω[x,y] and ω[jx,x]>0 if x∉K
  • if L is a compact subalgebra of G with jL⊆K+L then L⊆K

A j-algebra is a Lie algebra G with a subalgebra K and a linear map j satisfying the properties above.

The Lie algebra of a connected Lie group acting transitively on a homogeneous bounded domain is a j-algebra, which is not surprising as j-algebras are defined to have the obvious properties of such a Lie algebra. The converse is also true: any j-algebra is the Lie algebra of some transitive group of automorphisms of a homogeneous bounded domain. This does not give a 1:1 correspondence between homogeneous bounded domains and j-algebras, because a homogeneous bounded domain can have several different Lie groups acting transitively on it.

References

  • {{Citation | last1=Kaup | first1=Wilhelm | last2=Matsushima | first2=Yozô | last3=Ochiai | first3=Takushiro | title=On the automorphisms and equivalences of generalized Siegel domains | jstor=2373335 |mr=0267127 | year=1970 | journal=American Journal of Mathematics | issn=0002-9327 | volume=92 | pages=475–498 | doi=10.2307/2373335}}
  • {{Citation | last1=Murakami | first1=Shingo | title=On automorphisms of Siegel domains | publisher=Springer-Verlag | location=Berlin, New York | series=Lecture Notes in Mathematics | doi=10.1007/BFb0058567 |mr=0364690 | year=1972 | volume=286}}
  • {{Citation | last1=Piatetski-Shapiro | first1=I. I. | title=On a problem proposed by E. Cartan |mr=0101922 | year=1959 | journal=Doklady Akademii Nauk SSSR | issn=0002-3264 | volume=124 | pages=272–273}}
  • {{Citation | last1=Piatetski-Shapiro | first1=I. I. | title=Geometry of homogeneous domains and the theory of automorphic functions. The solution of a problem of E. Cartan|language=Russian | year=1959b | journal=Uspekhi Mat. Nauk | volume=14 | number=3|pages=190–192|url=http://www.mathnet.ru/php/archive.phtml?wshow=paper&jrnid=rm&paperid=7323}}
  • {{Citation | last1=Piatetski-Shapiro | first1=I. I. | title=Proc. Internat. Congr. Mathematicians (Stockholm, 1962) | url=http://mathunion.org/ICM/ICM1962.1/ | publisher=Inst. Mittag-Leffler | location=Djursholm | language=Russian | mr=0176105 | year=1963 | chapter=Domains of upper half-plane type in the theory of several complex variables | pages=389–396 | deadurl=yes | archiveurl=https://web.archive.org/web/20110717144510/http://mathunion.org/ICM/ICM1962.1/ | archivedate=2011-07-17 | df= }}
  • {{Citation | last1=Piatetski-Shapiro | first1=I. I. | title=Automorphic functions and the geometry of classical domains | origyear=1961 | url=https://books.google.com/books?id=gQmoAAAAIAAJ| publisher=Gordon and Breach Science Publishers | location=New York | series= Mathematics and Its Applications |mr=0136770 | year=1969 | volume=8}}
  • {{Citation | last1=Siegel | first1=Carl Ludwig | author1-link=Carl Ludwig Siegel | title=Einführung in die Theorie der Modulfunktionen n-ten Grades | doi=10.1007/BF01597381 |mr=0001251 | year=1939 | journal=Mathematische Annalen | issn=0025-5831 | volume=116 | pages=617–657}}
  • {{eom|id=s/s084990|first=E.B.|last= Vinberg}}
  • {{Citation | last1=Vinberg | first1=È. B. | last2=Gindikin | first2=S. G. | last3=Piatetski-Shapiro | first3=I. I. | title=Classification and canonical realization of complex homogeneous bounded domains |mr=0158415 | year=1963 | journal=Trudy Moskovskogo Matematičeskogo Obščestva | issn=0134-8663 | volume=12 | pages=359–388}} There is an English translation in the appendix of {{harv|Piatetski-Shapiro|1969}}.
  • {{Citation | last1=Xu | first1=Yichao | title=Theory of complex homogeneous bounded domains | url=https://books.google.com/books?id=KzqBHvRfQfYC | publisher=Science Press | location=Beijing | series=Mathematics and its Applications | isbn=978-1-4020-2132-9 |mr=2217650 | year=2005 | volume=569}}

1 : Complex manifolds
随便看

　

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。

　

Copyright © 2023 OENC.NET All Rights Reserved
京ICP备2021023879号 更新时间：2024/11/12 7:39:38