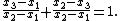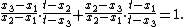“Siegel identity”的意思、由来-开放百科全书

词条

Siegel identity

释义

In mathematics, Siegel's identity refers to one of two formulae that are used in the resolution of Diophantine equations.

Statement

The first formula is

The second is

The identities are used in translating Diophantine problems connected with integral points on hyperelliptic curves into S-unit equations.

{{cite book | first=Alan | last=Baker | authorlink=Alan Baker (mathematician) | title=Transcendental Number Theory | publisher=Cambridge University Press | year=1975 | isbn=0-521-20461-5 | zbl=0297.10013 | page=40 }}
{{cite book | first1=Alan | last1=Baker | authorlink1=Alan Baker (mathematician)| first2=Gisbert | last2= Wüstholz | authorlink2=Gisbert Wüstholz | title=Logarithmic Forms and Diophantine Geometry | series=New Mathematical Monographs | volume=9 | publisher=Cambridge University Press | year=2007 | isbn=978-0-521-88268-2 | zbl=1145.11004 | page=53 }}
{{cite book | first1=Daniel S. | last1=Kubert | authorlink1=Daniel Kubert | first2=Serge | last2=Lang | authorlink2=Serge Lang | title=Modular Units | series= Grundlehren der Mathematischen Wissenschaften | volume=244 | year=1981 | isbn=0-387-90517-0 }}
{{cite book | first=Serge | last=Lang | authorlink=Serge Lang | title=Elliptic Curves: Diophantine Analysis | volume=231 | series=Grundlehren der mathematischen Wissenschaften | publisher=Springer-Verlag | year=1978 | isbn=0-387-08489-4 }}
{{cite book | title=The Algorithmic Resolution of Diophantine Equations | volume=41 | series=London Mathematical Society Student Texts | first=N. P. | last=Smart | authorlink=Nigel Smart (cryptographer) | publisher=Cambridge University Press | year=1998 | isbn=0-521-64633-2 | pages=36–37 }}

2 : Mathematical identities|Diophantine equations

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。