- Verlinde Formula
- Twisted Equivariant K-Theory
- See also
- Notes
- References
- External links
In mathematics, a Verlinde algebra is a finite-dimensional associative algebra introduced by {{harvs|txt|first=Erik|last=Verlinde|authorlink=Erik Verlinde|year=1988}}, with a basis of elements φλ corresponding to primary fields of a rational two-dimensional conformal field theory, whose structure constants N{{su|p=ν|b=λμ}} describe fusion of primary fields.
Verlinde Formula
In terms of the modular S-matrix, the fusion coefficients are given by[1]
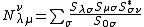
where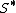 
is the component-wise complex conjugate of 
.
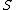Twisted Equivariant K-Theory
If G is a compact Lie group, there is a rational conformal field theory whose primary fields correspond to the representations λ of some fixed level of loop group of G. For this special case {{harvtxt|Freed, Hopkins and Teleman|2001}} showed that the Verlinde algebra can be identified with twisted equivariant K-theory of G.
See also
- Fusion rules
Notes
1. ^{{Cite book|url=https://www.worldcat.org/oclc/437345787|title=Introduction to Conformal Field Theory|last=Blumenhagen|first=Ralph|date=2009|publisher=Springer|others=Plauschinn, Erik|year=|isbn=9783642004490|location=Dordrecht|pages=143|oclc=437345787}}
References
- {{Citation | last1=Beauville | first1=Arnaud | editor1-last=Teicher | editor1-first=Mina|editor-link= Mina Teicher | title=Proceedings of the Hirzebruch 65 Conference on Algebraic Geometry (Ramat Gan, 1993) | url=http://math1.unice.fr/~beauvill/pubs/Hirz65.pdf | publisher=Bar-Ilan Univ. | location=Ramat Gan | series=Israel Math. Conf. Proc. | mr=1360497 | year=1996 | volume=9 | chapter=Conformal blocks, fusion rules and the Verlinde formula | pages=75–96}}
- {{Citation | last1=Bott | first1=Raoul | author1-link=Raoul Bott | title=On E. Verlinde's formula in the context of stable bundles | doi=10.1142/S0217751X91001404 | mr=1117752 | year=1991 | journal=International Journal of Modern Physics A | issn=0217-751X | volume=6 | issue=16 | pages=2847–2858|bibcode = 1991IJMPA...6.2847B }}
- {{Citation | last1=Faltings | first1=Gerd | title=A proof for the Verlinde formula | mr=1257326 | year=1994 | journal=Journal of Algebraic Geometry | issn=1056-3911 | volume=3 | issue=2 | pages=347–374}}
- {{Citation | last1=Freed | first1=Daniel S. | title=The Verlinde algebra is twisted equivariant K-theory | url=http://mistug.tubitak.gov.tr/bdyim/abs.php?dergi=mat&rak=0103-10 | mr=1829086 | year=2001 | journal=Turkish Journal of Mathematics | issn=1300-0098 | volume=25 | issue=1 | pages=159–167}}
- {{Citation | last1=Verlinde | first1=Erik | title=Fusion rules and modular transformations in 2D conformal field theory | doi=10.1016/0550-3213(88)90603-7 | mr=954762 | year=1988 | journal=Nuclear Physics B | issn=0550-3213 | volume=300 | issue=3 | pages=360–376|bibcode = 1988NuPhB.300..360V }}
- {{Citation | last1=Witten | first1=Edward | author1-link=Edward Witten | title=Geometry, topology, & physics | arxiv=hep-th/9312104 | publisher=Int. Press, Cambridge, MA | series=Conf. Proc. Lecture Notes Geom. Topology, IV | mr=1358625 | year=1995 | chapter=The Verlinde algebra and the cohomology of the Grassmannian | pages=357–422| bibcode=1993hep.th...12104W }}
External links
- {{citation|first=Erik Peter |last=Verlinde|url=http://www.scholarpedia.org/article/Verlinde_algebra|title=Verlinde algebra|journal=Scholarpedia}}
2 : Representation theory|Conformal field theory
- Minimum Information Required in the Annotation of Models
- Minimum Intelligent Signal Test
- Minimum interval takeoff
- Minimum Interval Take Off
- Minimum k-edge-connected spanning network problem
- Minimum k-node-connected spanning network problem
- Minimum (mathematics)
- Minimum Municipal Obligation
- Minimum Needs Programme (India)
- Minimum number of map colors
- Minimum overlap problem
- Minimum pay
- Minimum price
- Minimum rank of a graph
- Minimum Safe Altitude Warning
- Minimum spanning tree problem
- Minimum spanning trees
- Minimum Steiner tree
- Minimum Sudoku problem
- Minimum surface
- Minimum surface of revolution
- Minimum term
- Minimum track gauge
- Minimum viable population size
- Minimum Viable Product