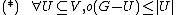“Tutte theorem”的意思、由来-开放百科全书

词条

Tutte theorem

释义

Tutte's theorem
Proofs
Direct proof Derivation from the Tutte-Berge formula
See also
Notes
References

In the mathematical discipline of graph theory the Tutte theorem, named after William Thomas Tutte, is a characterization of graphs with perfect matchings. It is a generalization of Hall's marriage theorem from bipartite to arbitrary graphs.{{Clarify|reason=how exactly is it a generalization?|date=February 2019}} It is a special case of the Tutte–Berge formula.

Tutte's theorem

A graph, {{math|G {{=}} (V, E)}}, has a perfect matching if and only if for every subset {{math|U}} of {{math|V}}, the subgraph induced by {{math|V − U}} has at most {{math||U|}} connected components with an odd number of vertices.^[1]

Proofs

Direct proof

First we write the condition:

where 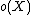denotes the number of odd components of the subgraph induced by .

Necessity of (∗): Consider a graph {{math|G}}, with a perfect matching. Let {{math|U}} be an arbitrary subset of {{math|V}}. Delete {{math|U}}. Let {{math|C}} be an arbitrary odd component in {{math|G − U}}. Since {{math|G}} had a perfect matching, at least one vertex in {{math|C}} must be matched to a vertex in {{math|U}}. Hence, each odd component has at least one vertex matched with a vertex in {{math|U}}. Since each vertex in {{math|U}} can be in this relation with at most one connected component (because of it being matched at most once in a perfect matching), {{math|o(G − U) ≤ {{!}}U{{!}}}}.^[2]

Sufficiency of (∗): Let {{math|G}} be an arbitrary graph with no perfect matching. We will find a bad set of vertices {{math|S}}, that is, a subset of {{math|V}} such that {{math|{{!}}S{{!}} < o(G − S)}}. We can suppose that {{math|G}} is edge-maximal, i.e., {{math|G + e}} has a perfect matching for every edge {{math|e}} not present in {{math|G}} already. Indeed, if we find a bad set {{math|S}} in edge-maximal graph {{math|G}}, then {{math|S}} is also a bad set in every spanning subgraph of {{math|G}}, as every odd component of {{math|G − S}} will be split into possibly more components at least one of which will again be odd.

We define {{math|S}} to be the set of vertices with degree {{math|{{!}}V{{!}} − 1}}. First we consider the case where all components of {{math|G − S}} are complete graphs. Then {{math|S}} has to be a bad set, since if {{math|o(G − S) ≤ {{!}}S{{!}}}}, then we could find a perfect matching by matching one vertex from every odd component with a vertex from {{math|S}} and pairing up all other vertices (this will work unless {{math|{{!}}V{{!}}}} is odd, but then {{math|∅}} is bad).

Now suppose that {{math|K}} is a component of {{math|G − S}} and {{math|x, y ∈ K}} are vertices such that {{math|xy ∉ E}}. Let {{math|x, a, b ∈ K}} be the first vertices on a shortest {{math|x,y}}-path in {{math|K}}. This ensures that {{math|xa, ab ∈ E}} and {{math|xb ∉ E}}. Since {{math|a ∉ S}}, there exists a vertex {{math|c}} such that {{math|ac ∉ E}}. From the edge-maximality of {{math|G}}, we define {{math|M₁}} as a perfect matching in {{math|G + xb}} and {{math|M₂}} as a perfect matching in {{math|G + ac}}. Observe that surely {{math|xb ∈ M₁}} and {{math|ac ∈ M₂}}.

Let {{math|P}} be the maximal path in {{math|G}} that starts from {{math|c}} with an edge from {{math|M₁}} and whose edges alternate between {{math|M₁}} and {{math|M₂}}. How can {{math|P}} end? Unless we are arrive at 'special' vertex such as {{math|x, a}} or {{math|b}}, we can always continue: {{math|c}} is {{math|M₂}}-matched by {{math|ca}}, so the first edge of {{math|P}} is not in {{math|M₂}}, therefore the second vertex is {{math|M₂}}-matched by a different vertex and we continue in this manner.

Let {{math|v}} denote the last vertex of {{math|P}}. If the last edge of {{math|P}} is in {{math|M₁}}, then {{math|v}} has to be {{math|a}}, since otherwise we could continue with an edge from {{math|M₂}} (even to arrive at {{math|x}} or {{math|b}}). In this case we define {{math|C:{{=}}P + ac}}. If the last edge of {{math|P}} is in {{math|M₂}}, then surely {{math|v ∈ {x, b}}} for analogous reason and we define {{math|C:{{=}}P + va + ac}}.

Now {{math|C}} is a cycle in {{math|G + ac}} of even length with every other edge in {{math|M₂}}. We can now define {{math|M:{{=}}M₂ Δ C}} (where {{math|Δ}} is symmetric difference) and we obtain a matching in {{math|G}}, a contradiction.

Derivation from the Tutte-Berge formula

The Tutte–Berge formula says that the size of a maximum matching of a graph equals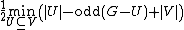

Tutte's condition is that, for every 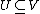, 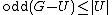. Equivalently, the expression inside the minimum is at least |V|. Equivalently, the entire expression is at least |V|/2.

So, Tutte's condition holds iff the graph has a matching of size at least |V|/2, iff the graph has a perfect matching.

Notes

1. ^{{harvtxt |Lovász|Plummer|1986}}, p. 84; {{harvtxt|Bondy|Murty|1976}}, Theorem 5.4, p. 76.
2. ^{{harvtxt|Bondy|Murty|1976}}, pp. 76–78.

References

{{Cite book

| last=Bondy | first=J. A.
| last2=Murty | first2=U. S. R.
| title=Graph theory with applications | year=1976 | publisher=American Elsevier Pub. Co. | location=New York | isbn=0-444-19451-7|ref=harv}}

{{Cite book

| last1=Lovász | first1=László | author1-link=László Lovász
| last2=Plummer | first2=M. D. | author2-link=Michael D. Plummer
| title=Matching theory | year=1986 | publisher=North-Holland | location=Amsterdam | isbn=0-444-87916-1|ref=harv}}

3 : Matching|Theorems in graph theory|Articles containing proofs

随便看