- Contributions
- Selected publications
- References
Ilona Palásti (1924–1991) was a Hungarian mathematician who worked at the Alfréd Rényi Institute of Mathematics. She is known for her research in discrete geometry, geometric probability, and the theory of random graphs.{{r|fmi}}
With Alfréd Rényi and others, she was considered to be one of the members of the Hungarian School of Probability.{{r|leading}}
Contributions
In connection to the Erdős distinct distances problem, Palásti studied the existence of point sets for which the  th least frequent distance occurs
th least frequent distance occurs  times. That is, in such points there is one distance that occurs only once, another distance that occurs exactly two times, a third distance that occurs exactly three times, etc. For instance, three points with this structure must form an isosceles triangle. Any
times. That is, in such points there is one distance that occurs only once, another distance that occurs exactly two times, a third distance that occurs exactly three times, etc. For instance, three points with this structure must form an isosceles triangle. Any  evenly-spaced points on a line or circular arc also have the same property, but Paul Erdős asked whether this is possible for points in general position (no three on a line, and no four on a circle). Palásti found an eight-point set with this property, and showed that for any number of points between three and eight (inclusive) there is a subset of the hexagonal lattice with this property. Palásti's eight-point example remains the largest known.{{r|pano|bicycle}}{{ran|E}}
evenly-spaced points on a line or circular arc also have the same property, but Paul Erdős asked whether this is possible for points in general position (no three on a line, and no four on a circle). Palásti found an eight-point set with this property, and showed that for any number of points between three and eight (inclusive) there is a subset of the hexagonal lattice with this property. Palásti's eight-point example remains the largest known.{{r|pano|bicycle}}{{ran|E}}
Another of Palásti's results in discrete geometry concerns the number of triangular faces in an arrangement of lines. When no three lines may cross at a single point, she and Zoltán Füredi found sets of  lines, subsets of the diagonals of a regular
lines, subsets of the diagonals of a regular  -gon, having
-gon, having  triangles. This remains the best lower bound known for this problem, and differs from the upper bound by only
triangles. This remains the best lower bound known for this problem, and differs from the upper bound by only 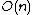 triangles.{{r|pano}}{{ran|D}}
triangles.{{r|pano}}{{ran|D}}
In geometric probability, Palásti is known for her conjecture on random sequential adsorption, also known in the one-dimensional case as "the parking problem". In this problem, one places non-overlapping balls within a given region, one at a time with random locations, until no more can be placed. Palásti conjectured that the average packing density in  -dimensional space could be computed as the
-dimensional space could be computed as the  th power of the one-dimensional density.{{r|craft}} Although her conjecture led to subsequent research in the same area, it has been shown to be inconsistent with the actual average packing density in dimensions two through four.{{r|bs}}{{ran|A}}
th power of the one-dimensional density.{{r|craft}} Although her conjecture led to subsequent research in the same area, it has been shown to be inconsistent with the actual average packing density in dimensions two through four.{{r|bs}}{{ran|A}}
Palásti's results in the theory of random graphs include bounds on the probability that a random graph has a Hamiltonian circuit, and on the probability that a random directed graph is strongly connected.{{r|rg}}{{ran|B}}{{ran|C}}
Selected publications
{{rma|A|{{citation| last = Palásti | first = Ilona
| journal = Magyar Tud. Akad. Mat. Kutató Int. Közl.
| mr = 0146947
| pages = 353–360
| title = On some random space filling problems
| volume = 5
| year = 1960}}}}{{rma|B|{{citation
| last = Palásti | first = I.
| journal = Studia Scientiarum Mathematicarum Hungarica
| mr = 0207588
| pages = 205–214
| title = On the strong connectedness of directed random graphs
| volume = 1
| year = 1966}}}}{{rma|C|{{citation
| last = Palásti | first = I.
| doi = 10.1007/BF02029168
| issue = 2
| journal = Periodica Mathematica Hungarica
| mr = 0285437
| pages = 107–112
| title = On Hamilton-cycles of random graphs
| volume = 1
| year = 1971}}}}{{rma|D|{{citation
| last1 = Füredi | first1 = Z. | author1-link = Zoltán Füredi
| last2 = Palásti | first2 = I.
| doi = 10.2307/2045427
| issue = 4
| journal = Proceedings of the American Mathematical Society
| mr = 760946
| pages = 561–566
| title = Arrangements of lines with a large number of triangles
| volume = 92
| year = 1984}}}}{{rma|E|{{citation
| last = Palásti | first = I.
| doi = 10.1007/BF01848126
| issue = 3
| journal = Periodica Mathematica Hungarica
| mr = 1028960
| pages = 231–235
| title = Lattice-point examples for a question of Erdős
| volume = 20
| year = 1989}}}}
References
2. ^{{citation | last = Solomon | first = Herbert | authorlink = Herbert Solomon | editor-last = Gani | editor-first = J. M. | contribution = Looking at life quantitatively | doi = 10.1007/978-1-4613-8631-5_2 | isbn = 0-387-96277-8 | location = New York | mr = 861127 | pages = 10–30 | publisher = Springer-Verlag | series = Applied Probability | title = The craft of probabilistic modelling: A collection of personal accounts | year = 1986}}. See in particular [https://books.google.com/books?id=je_lBwAAQBAJ&pg=PA23 p. 23].
3. ^{{citation|url=https://old.renyi.hu/former_new.html|title=Former Members of the Institute|publisher=Alfréd Rényi Institute of Mathematics|accessdate=2018-09-13}}.
4. ^{{citation | last1 = Johnson | first1 = Norman L. | author1-link = Norman Lloyd Johnson | last2 = Kotz | first2 = Samuel | author2-link = Samuel Kotz | contribution = Rényi, Alfréd | doi = 10.1002/9781118150719.ch62 | isbn = 0-471-16381-3 | mr = 1469759 | pages = 205–207 | publisher = John Wiley & Sons | location = New York | series = Wiley Series in Probability and Statistics: Probability and Statistics | title = Leading personalities in statistical sciences: From the seventeenth century to the present | year = 1997}}. See in particular [https://books.google.com/books?id=AzZZ-uW6WuEC&pg=PA205 p. 205].
5. ^{{citation | last = Bárány | first = Imre | authorlink = Imre Bárány | editor-last = Horváth | editor-first = János | contribution = Discrete and convex geometry | doi = 10.1007/978-3-540-30721-1_14 | mr = 2547518 | pages = 427–454 | publisher = Springer, Berlin | series = Bolyai Soc. Math. Stud. | title = A panorama of Hungarian mathematics in the twentieth century. I | volume = 14 | year = 2006}} See in particular [https://books.google.com/books?id=EWm4WzSaG3IC&pg=PA444 p. 444] and [https://books.google.com/books?id=EWm4WzSaG3IC&pg=PA44 p. 449].
6. ^{{citation | last = Bollobás | first = Béla | authorlink = Béla Bollobás | doi = 10.1017/CBO9780511814068 | edition = 2nd | isbn = 0-521-80920-7 | mr = 1864966 | publisher = Cambridge University Press | location = Cambridge, UK | series = Cambridge Studies in Advanced Mathematics | title = Random graphs | volume = 73 | year = 2001}}. See in particular [https://books.google.com/books?id=o9WecWgilzYC&pg=PA198 p. 198] and [https://books.google.com/books?id=o9WecWgilzYC&pg=PA201 p. 201].
}}{{Authority control}}{{DEFAULTSORT:Palasti, Ilona}}
- American academy of cosmetic dentistry
- American Academy of Craniofacial Pain
- American academy of craniofacial pain
- American academy of dermatology
- American academy of diplomacy
- American Academy of Diplomacy
- American Academy of Disaster Medicine
- American academy of dramatic arts
- American Academy of Facial, Plastic and Reconstructive Surgery
- American Academy of Facial Plastic and Reconstructive Surgery
- American academy of facial plastic and reconstructive surgery
- American academy of family physicians
- American Academy of Financial Management
- American academy of financial management
- American Academy of Forensic Science
- American academy of forensic sciences
- American academy of hospitality sciences
- American Academy of Hospitality Sciences
- American Academy of Larnaca
- American academy of larnaca
- American Academy of Liberal Education
- American Academy of Motion Picture Arts and Sciences
- American academy of neurology
- American Academy of Neurology
- American Academy of Nursing