“8-demicube”的意思、由来-开放百科全书

词条

8-demicube

释义

Cartesian coordinates
Related polytopes and honeycombs
Images
References
External links

Demiocteract (8-demicube)
Petrie polygon projection
Type	Uniform 8-polytope
Family	demihypercube
Coxeter symbol	1₅₁
Schläfli symbols	{3,3^5,1} = h{4,3⁶} s{2^{1,1,1,1,1,1,1}}
Coxeter diagrams	nodes_10ru\|split2\|node\|3\|node\|3\|node\|3\|node\|3\|node\|3\|node}} = {{CDD\|node_h1\|4\|node\|3\|node\|3\|node\|3\|node\|3\|node\|3\|node\|3\|node}} {{CDD\|node_h\|2x\|node_h\|4\|node\|3\|node\|3\|node\|3\|node\|3\|node\|}} {{CDD\|node_h\|2x\|node_h\|2x\|node_h\|4\|node\|3\|node\|3\|node\|3\|node\|3\|node\|}} {{CDD\|node_h\|2x\|node_h\|2x\|node_h\|2x\|node_h\|4\|node\|3\|node\|3\|node\|3\|node\|}} {{CDD\|node_h\|2x\|node_h\|2x\|node_h\|2x\|node_h\|2x\|node_h\|4\|node\|3\|node\|3\|node\|}} {{CDD\|node_h\|2x\|node_h\|2x\|node_h\|2x\|node_h\|2x\|node_h\|2x\|node_h\|4\|node\|3\|node\|}} {{CDD\|node_h\|2x\|node_h\|2x\|node_h\|2x\|node_h\|2x\|node_h\|2x\|node_h\|2x\|node_h\|4\|node\|}} {{CDD\|node_h\|2x\|node_h\|2x\|node_h\|2x\|node_h\|2x\|node_h\|2x\|node_h\|2x\|node_h\|2x\|node_h}}
7-faces	144: 16 {3^1,4,1} 128 {3⁶}
6-faces	112 {3^1,3,1} 1024 {3⁵}
5-faces	448 {3^1,2,1} 3584 {3⁴}
4-faces	1120 {3^1,1,1} 7168 {3,3,3}
Cells	10752: 1792 {3^1,0,1} 8960 {3,3}
Faces	7168 {3}
Edges	1792
Vertices	128
Vertex figure	Rectified 7-simplex
Symmetry group	D₈, [3^5,1,1] = [1⁺,4,3⁶] A₁⁸, [2⁷]⁺
Dual	?
Properties	convex

In geometry, a demiocteract or 8-demicube is a uniform 8-polytope, constructed from the 8-hypercube, octeract, with alternated vertices removed. It is part of a dimensionally infinite family of uniform polytopes called demihypercubes.

E. L. Elte identified it in 1912 as a semiregular polytope, labeling it as HM₈ for an 8-dimensional half measure polytope.

Coxeter named this polytope as 1₅₁ from its Coxeter diagram, with a ring on

one of the 1-length branches, {{CDD|node_1|3|node|split1|nodes|3a|nodea|3a|nodea|3a|nodea|3a|nodea}} and Schläfli symbol 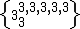or {3,3^5,1}.

Cartesian coordinates

Cartesian coordinates for the vertices of an 8-demicube centered at the origin are alternate halves of the 8-cube:

(±1,±1,±1,±1,±1,±1,±1,±1)

with an odd number of plus signs.

Related polytopes and honeycombs

This polytope is the vertex figure for the uniform tessellation, 2₅₁ with Coxeter-Dynkin diagram:

{{CDD|nodea_1|3a|nodea|3a|branch|3a|nodea|3a|nodea|3a|nodea|3a|nodea|3a|nodea}}

Images

References

H.S.M. Coxeter:
- Coxeter, Regular Polytopes, (3rd edition, 1973), Dover edition, {{ISBN|0-486-61480-8}}, p. 296, Table I (iii): Regular Polytopes, three regular polytopes in n-dimensions (n≥5)
- H.S.M. Coxeter, Regular Polytopes, 3rd Edition, Dover New York, 1973, p. 296, Table I (iii): Regular Polytopes, three regular polytopes in n-dimensions (n≥5)
- Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, {{ISBN|978-0-471-01003-6}}
- (Paper 22) H.S.M. Coxeter, Regular and Semi Regular Polytopes I, [Math. Zeit. 46 (1940) 380-407, MR 2,10]
- (Paper 23) H.S.M. Coxeter, Regular and Semi-Regular Polytopes II, [Math. Zeit. 188 (1985) 559-591]
- (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3-45]
John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, The Symmetries of Things 2008, {{ISBN|978-1-56881-220-5}} (Chapter 26. pp. 409: Hemicubes: 1_n1)

External links

{{GlossaryForHyperspace | anchor=half | title=Demiocteract }}
Multi-dimensional Glossary

1 : 8-polytopes

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。