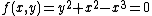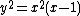1. See also

2. References

An acnode is an isolated point in the solution set of a polynomial equation in two real variables. Equivalent terms are "isolated point or hermit point".^[1]

For example the equation

has an acnode at the origin, because it is equivalent to

and 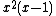is non-negative only when ≥ 1 or . Thus, over the real numbers the equation has no solutions for 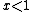except for (0, 0).

In contrast, over the complex numbers the origin is not isolated since square roots of negative real numbers exist. In fact, the complex solution set of a polynomial equation in two complex variables can never have an isolated point.

An acnode is a critical point, or singularity, of the defining polynomial function, in the sense that both partial derivatives 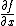and 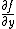vanish. Further the Hessian matrix of second derivatives will be positive definite or negative definite, since the function must have a local minimum or a local maximum at the singularity.

See also

• Singular point of a curve
• Crunode
• Cusp
• Tacnode

References

• {{cite book |last=Porteous |first=Ian |title=Geometric Differentiation |year=1994 |publisher=Cambridge University Press |isbn=0-521-39063-X }}

• Malesherbiaceae
• Maleshevo Mountain
• Malesiada
• Malesia (disambiguation)
• Malesia, Montenegro
• Malesian frog
• Malesian Region
• Malesi e Madhe
• Malesija
• Malesija, Montenegro
• Malesina
• Malesk
• Male skirt
• Male soprano
• Malesori
• Malesov
• Male Srakane
• Malesso
• Malestan
• Malestan District
• Male Straciny
• Male Strikebreaker
• Male stripper
• Malestroit
• Malesub