053 圆周率
圆周与其直径的长度比。该比值是一常数,以希腊字母π记之。圆周率是人类认识到的第一个特殊常数。对于圆周率的研究,在一定程度上能够反映一个时代或一个民族的数学发展水平。中国古代数学家在圆周率的研究方面有着杰出的成就,对世界数学的发展作出了卓越贡献。
早在远古时,中国先民已认识到圆周长与其直径的比值是一个常数。不晚于公元前3世纪成书的《墨经》中已有“小圆之圆与大圆之圆同”的记载。直至 《九章算术》成书为止,一直沿用“径一周三”的古率。1世纪初,刘歆造律嘉量斛,取π=3.1547,后人称“歆率”。2世纪初,张衡计算球体积时,在世界上最早使用了π=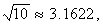 曾取π=730/232≈3.1466。三国时吴人王蕃在浑议论说中取π=142/45≈3.1556。圆周率的精确度渐有提高。但以上均属经验值。3世纪,刘徽在《九章算术注》中创立“割圆术”。为计算圆周率提供了理论依据和严密的科学方法。刘徽运用极限思想得到圆内接正多边形的面积序列的不等式
曾取π=730/232≈3.1466。三国时吴人王蕃在浑议论说中取π=142/45≈3.1556。圆周率的精确度渐有提高。但以上均属经验值。3世纪,刘徽在《九章算术注》中创立“割圆术”。为计算圆周率提供了理论依据和严密的科学方法。刘徽运用极限思想得到圆内接正多边形的面积序列的不等式
S2n圆n+2(S2n-Sn),并证明了圆面积等于半周乘以半径。在此基础上,他从半径为1尺的圆内接正6边形开始,逐次割圆,使边数倍增,直至求出圆内接正96边、192边形面积。利用公式
S192圆96+2 (S192-S96)
求得
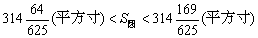 。舍弃分数部分,取S圆=314平方寸,得π=3.14=157/50,后人称“徽率”。这是当时世界上圆周率的最佳值。在计算圆周率的历史上占有重要地位。进而求出π=3927/1250≈3.1416。5世纪,据推测,祖冲之运用割圆术进一步求出
。舍弃分数部分,取S圆=314平方寸,得π=3.14=157/50,后人称“徽率”。这是当时世界上圆周率的最佳值。在计算圆周率的历史上占有重要地位。进而求出π=3927/1250≈3.1416。5世纪,据推测,祖冲之运用割圆术进一步求出3.1415926<π<3.1415927,
并以22/7为约率,355/113为密率,使中国在圆周率计算方面在世界上领先1100年之久。
对于圆周率的其他方面的研究,中国数学家也作了一定的工作。清代蒙古族数学家明安图 (约1691—约1768)利用自创的割圆连比例法独立证明了牛顿在1676年得到的公式:
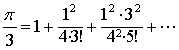 ,清代数学家项明达(1789-1850)在推导椭圆公式时得到圆周率的倒数公式:
,清代数学家项明达(1789-1850)在推导椭圆公式时得到圆周率的倒数公式: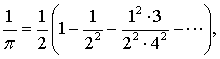
李善兰利用他所创的尖锥术,求得
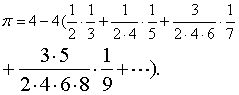
圆周率yuanzhoulu
圆的周长与直径的比.通常圆周率用希腊字母π表示.圆周率是一个无限不循环小数(无理数),π=3.141 592 653 5….
我国古代的数学家对于圆周率的研究有过很突出的贡献.尤其是宋代的祖冲之,计算结果更为精密.祖冲之求得:
3.141 592 6<π<3.141 592 7.
并用22/7和355/113作为π的近似值.其中22/7称为约率,355/113称为密率.密率355/113=3.141 592 920…,它与π的误差小于0.000 001.
圆周率Yuanzhoulu
圆的周长和它的直径的比。圆周率是一个无限不循环小数, 通常用希腊字母π来表示, π=3.14159265……。
在已知半径为r的圆内,作内接正六边形,把六边形的边数加倍,得到圆内接正十二边形;再加倍,得到圆内接正二十四边形, ……我们把这样一些正多边形的周长,看作是圆的周长的近似值。把圆内接正多边形的周长与直径的比, 作为圆的周长与直径的比的近似值。当圆内接正多边形的边数不断地成倍增加时,它们的周长pn不断地增大,越来越接近于圆的周长,圆内接正多边形的周长pn和直径2r的比值, 就越来越接近于圆周长c和直径2r的比值,误差越来越小。只要圆内接正多边形的边数n充分大,误差可以任意地小。
设圆内接正六边形的边长a6=r,an、a2n分别表示圆内接正n边形和正2n边形的边长。根据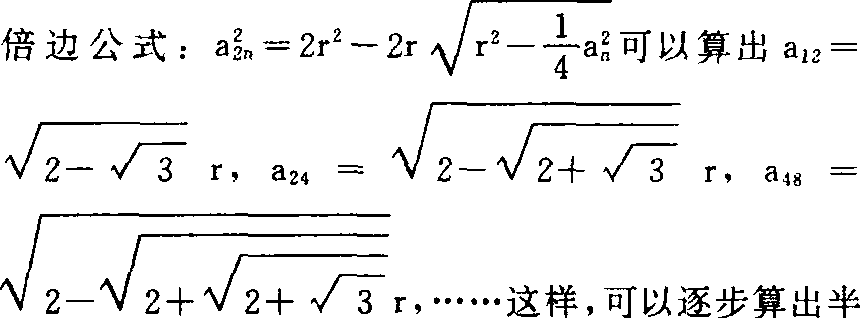
径为r的圆内接正6、12、24、……边形的边长、周长以及周长与直径的比 (见下表):
| n | 边长an | 周长pn | pn/2r |
| 6 12 24 48 96 192 384 768 | 1.00000000r 0.51763809r 0.26105238r 0.13080626r 0.06543817r 0.03272346r 0.01636228r 0.00818121r | 6.00000000r 6.21165708r 6.26525722r 6.27870041r 6.28206396r 6.28290510r 6.28311544r 6.28316941r | 3.00000000 3.10582854 3.13262861 3.13935021 3.14103198 3.14145255 3.14155772 3.14158471 |
这样, 我们就得到了一种计算圆周率π的近似值的方法。
我国南北朝时期的数学家祖冲之, 在公元五世纪就已经算得π的值在3.1415926与3.1415927之间,比其它国家早一千年左右。他首创用22/7和355/113作为π的近似值, 其中22/7称为约率, 355/113称为密率, 密率355/113=3.141592920……, 与π的误差小于0.000001。
圆周率Yuan zhou lu
圆是人类最早认识的几何图形之一。通过对圆面积、圆周长的各种实际测量古人很早就发现,圆的面积与其半径的平方成正比:S=π1r2, 其中π1是某个常数; 圆的周长和它的直径成正比: C=π2d, 其中π2是某个常数。人们还发现, π1和π2都近似地等于3。最早在数学上严格证明π1=π2=π, 并且给出求π值的严密算法的是古希腊数学家阿基米德(公元前287—前212,参见该条及“割圆术”)。在中国,《九章算术》中已经明确地认识到了上述事实,公元3世纪刘徽给出了严格证明。
由于π是希腊文περιφξρια(圆周)的第一个字母,δ是δι′αμεてρου(直径)的第一个字母,英国数学家奥特雷德(Oughtred. W.1574—1660)1647年用S/π表示直径与圆周之比。英国数学家琼斯(Jones, W. ,)于1706年最先明确地用π代表圆周与直径之比,即圆周率。1737年欧拉采纳了这个符号,从此人们便逐渐用π表示圆周率了。
对圆周率π的研究,包括其数值、性质与公式等,是数学史上最悠久、最奇特、最富有思想、也是最能体现数学进步的主题之一, 不少学者把π值计算及对π的研究做为衡量古代数学发展水平的标准之一。
在数学发展的早期,人们是通过实验、度量的方式得到粗略的π值的,在漫长的年代里它被取作了。大约公元前1650年, 埃及人得到了一个较好的近似值(16/9)2。历史上对π的研究第一个具有决定性意义的进
步是公元前5世纪希腊人发明了割圆术 (参见该条),而阿基米德以及后来的中国数学家刘徽都给出了由此计算π值的严格数学方法。1593年,法国数学家韦达(参见该条) 给出了π的第一个解析表达式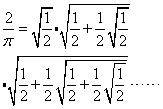
从此对π的研究进入了解析的时代,1674年,德国数学家莱布尼茨(参见该条)首次给出了关于π的一个十分优美的无穷级数表达式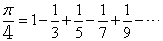
在1946年电子计算机投入使用之后,利用计算机对π进行研究立即扩大了人们的视野, 使之进入了一个崭新的阶段。
对π的研究方法的每一次重大变革, 都在长时间里推动了更精确的π值计算。利用割圆术,阿基米德得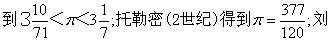
徽给出π=3.1416; 祖冲之很可能也是利用割圆术得到3. 1415926<π<3.1415927;最高纪录是1630年格林伯根求出的39位小数(参见“割圆术”)。利用解析方法,英国数学家夏普(Sharp, A.)于1699年求至71位小数; 梅钦(Machin, J. 英国, 1706)求至100位小数; 达泽Dase. J. M. Z.,德国1844求至200位小数;尚克斯(Shanks,英国,1873)花费20多年时间求至707位小数, 可惜在第528位上把4错误地求为5,以下的各位小数全部无效;1946年,美国数学家佛格森(Ferguson)发现了这一错误,次年求得正确的710位小数;1949年,美国数学家伦奇(Wrench,J. W.)与史密斯(Smith,L. B.)合作算至1 120位小数, 创解析方法求π值的最高纪录。
1949年, 麦雷兰德 (Maryland, 美国) 利用世界上第一台投入使用的电子计算机ENIAC将π值计算到2 037位小数,这是利用计算机研究π值的第一个结果。此后,π值的精确度迅速提高:1959年,16 167位小数 (裘努埃, 法国); 1961年, 100 265位小数 (伦奇, 尚克斯,美国); 1973年, 100万位 (纪劳德, 法国); 1987年, 134 217 728位小数 (金田安政, 日本)。到1989年, π值已突破了10亿位小数大关。
对π的性质的认识也在不断地深化着。1748年,大数学家欧拉给出eiπ+1=0这一极为优美的关系式,并猜测π是超越数; 1761年, 德国数学家兰伯特(Lambert,J. H.)证明了π是无理数;1882年,林德曼 (Lindemann,C. L. F., 德国)证明π是超越数,从而彻底解决了困扰人们2000多年的化圆为方问题;1977年, 哈肯 (Haken,W., 美国)猜测π的前几位数决不能成为完全平方数。此外, 在π的小数第710100位开始, 出现了3 333 333, 另一串7个3从第3 204 765位开始出现; 从第995 998位开始出现了上升数列23 456 789,而下降数列876 543 210开始于第2 747 956位。但至今尚不知道π的十进小数表达中是否会出现序列0 123 456789。
有关π的研究工作及其研究者如此之多。涉及范围如此之广,持续时间如此之长,正如一位英国数学家所说:“这个奇妙的3.14159溜进了每一扇门,冲进了每一扇窗, 钻进了每一个烟囱。”
圆周率
数学名词。平面几何中圆周与其直径的长度之比,它是一个无理数。这是人类认识到的第1个常数。欧几里得的《几何原本》中已提到过它是常数,中国古代也早有“径一周三”的说法,即认为圆周率的近似值为3。用π表示圆周率始于欧拉(1737年)。通常以3.1416作为π的有理近似值,对日常计算这已足够精确。三国时期刘徽得出所谓徽率为3.14;南北朝时祖冲之得出圆周率在3.1415926与3.1415927之间,并提出约率为22/7,密率(也称为祖率)355/113(精确到0.000001)。这比西方最早得出这个近值早了1100年。圆周率小数取至100位时,为3.141 592 653 589 793 238 462 643 383 279 502 884 197 169 399 375 105 820 974 944 592 307 816 406 286 208 998 628 034 825 342 117 068 0(小数点后第97位起,尾数原为067 982 148…,截取100位小数时,进位才成068 0)。有些科学家用熟练背诵此数来训练记忆,锻炼思维。每年3月14日为世界π日。2005年11月19~20日,中国学生吕超连续无差错地背诵出π小数67890位,创下吉尼斯纪录。