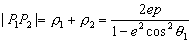圆锥曲线的极坐标方程yuanzhui quxian de jizuobiaofangcheng
一动点P到一定点O的距离与到一定直线l的距离之比为一常数e，则P点的轨迹为圆锥曲线.
以定点O为极点，极轴垂直于定直线，建立极坐标系如图.设O点到l的距离为p，则P点的轨迹方程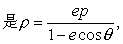
这就是圆锥曲线的极坐标方程.
注意：
❶e为离心率，当0
❷p为焦点到同侧准线的距离，即焦准距.ep的数值等于圆锥曲线的通径（又称正焦弦）长度之半；
❸与这个极坐标方程对应的直角坐标系方程是(1-e2)x2+y2-2e2px-e2p2＝0.从这里经过配方整理易得当e≠1时，椭圆（或双曲线）的半长轴（或半实轴）a，半短轴（或半虚轴）b，半焦距c等与参数e,p之间的关系式.即当e≠1时
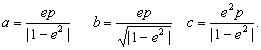
❹利用这个极坐标方程，容易求得焦点弦（经过焦点的弦）P1P2的长.若知P1n(ρ1,θ1),P2 (ρ2,θ1+
| π), |
| 则 |
