078 垛积术

高阶等差级数的求和方法。对于一阶等差级数，古已早有研究。《九章算术》已给出等差级数通项求法。《张丘建算经》给出了等差级数求和公式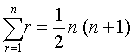：。对高阶等差级数的研究，则自沈括始。其所创“隙积术”即二阶等差级数求和方法。他给出了长方台垛的垛积公式——沈括公式。南宋著名数学家杨辉的研究丰富了隙积术的成果。其所撰《详解九章算法》、《算法通变本末》给出了：

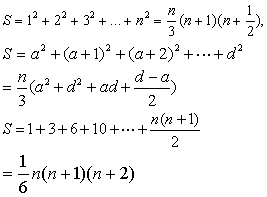
三个垛积公式。它们实际上是沈括公式的几个特列。一般地，称杨辉及其后的高阶等差级数求和方法为“垛积术”。元朱世杰发展了沈括的隙积术，对垛积术进行了详细、系统的研究，得出了一般性的结论。朱世杰研究了分别以等差级数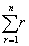的和、二阶等差级数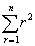的和为一般项的两类级数，并连续以新级数的和为一般项推出另一新的高阶等差级数的求和公式。他给出公式：
(1)三角垛：
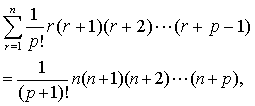
(2)岚峰形垛：
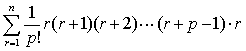
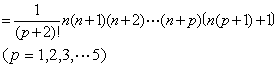
在(1)中，依次取p=1,2，…就得到一个三角垛积公式序列。其中后一公式恰是以前一公式的结果为一般项的新级数的求和公式。就垛积而言，就是：前式的三角垛中至第r+1层为止的垛积正是后式的三角垛中的第r层。清陈世仁(1676-1722)在其垛积术专论《少广拾遗》中又给出

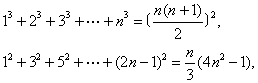
1³+3³+5³+…+(2n-1)³＝n²(2n²-1)
等12类37个垛积公式及其变形。李善兰对三角垛、乘方垛、三角相乘垛及三角变垛等求和问题进行了深入、全面地研究。发现了包括“幂和公式”(求前n个自然数的方幂和的公式)与著名的“李善兰恒等式”在内的多种类型的代数恒等式。其成果集中于所撰《垛积比类》之中。