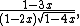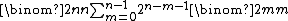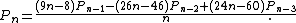“Skew-merged permutation”的意思、由来-开放百科全书

词条

Skew-merged permutation

释义

Characterization
Enumeration
Computational complexity
References

In the theory of permutation patterns, a skew-merged permutation is a permutation that can be partitioned into an increasing sequence and a decreasing sequence. They were first studied by {{harvtxt|Stankova|1994}} and given their name by {{harvtxt|Atkinson|1998}}.

Characterization

The two smallest permutations that cannot be partitioned into an increasing and a decreasing sequence are 3412 and 2143. {{harvtxt|Stankova|1994}} was the first to establish that a skew-merged permutation can also be equivalently defined as a permutation that avoids the two patterns 3412 and 2143.

A permutation is skew-merged if and only if its associated permutation graph is a split graph, a graph that can be partitioned into a clique (corresponding to the descending subsequence) and an independent set (corresponding to the ascending subsequence). The two forbidden patterns for skew-merged permutations, 3412 and 2143, correspond to two of the three forbidden induced subgraphs for split graphs, a four-vertex cycle and a graph with two disjoint edges, respectively. The third forbidden induced subgraph, a five-vertex cycle, cannot exist in a permutation graph (see {{harvtxt|Kézdy|Snevily|Wang|1996}}).

Enumeration

For 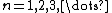the number of skew-merged permutations of length is

1, 2, 6, 22, 86, 340, 1340, 5254, 20518, 79932, 311028, 1209916, 4707964, 18330728, ... {{OEIS|A029759}}.

{{harvtxt|Atkinson|1998}} was the first to show that the generating function of these numbers is

from which it follows that the number of skew-merged permutations of length is given by the formula

and that these numbers obey the recurrence relation

Another derivation of the generating function for skew-merged permutations was given by {{harvtxt|Albert|Vatter|2013}}.

Computational complexity

Testing whether one permutation is a pattern in another can be solved efficiently when the larger of the two permutations is skew-merged, as shown by {{harvtxt|Albert|Lackner|Lackner|Vatter|2016}}.

References

{{citation

| last1 = Albert | first1 = Michael
| author1-link=Michael H. Albert
| last2 = Vatter | first2 = Vincent
| journal = Electronic Journal of Combinatorics
| mr = 3084586
| volume = 20
| number = 2
| pages = Paper 44, 11 pp.
| title = Generating and enumerating 321-avoiding and skew-merged simple permutations
| url = http://www.combinatorics.org/ojs/index.php/eljc/article/view/v20i2p44
| year = 2013}}.

{{citation

| last1 = Albert | first1 = Michael
| author1-link=Michael H. Albert
| last2 = Lackner | first2 = Marie-Louise
| last3 = Lackner | first3 = Martin
| last4 = Vatter | first4 = Vincent
| arxiv = 1510.06051
| bibcode = 2015arXiv151006051A
| department = Permutation Patterns 2015
| issue = 2
| journal = Discrete Mathematics & Theoretical Computer Science
| mr = 3597961
| pages = P11:1–17
| title = The complexity of pattern matching for 321-avoiding and skew-merged permutations
| url = https://dmtcs.episciences.org/2607
| volume = 18
| year = 2016}}.

{{citation

| last = Atkinson | first = M. D.
| journal = Electronic Journal of Combinatorics
| mr = 1490467
| pages = RP6:1–13
| title = Permutations which are the union of an increasing and a decreasing subsequence
| url = https://www.combinatorics.org/Volume_5/Abstracts/v5i1r6.html
| volume = 5
| year = 1998}}. See also the attached comment by Volker Strehl.

{{citation

| last1 = Kézdy | first1 = André E.
| last2 = Snevily | first2 = Hunter S.
| last3 = Wang | first3 = Chi
| doi = 10.1016/S0097-3165(96)80012-4
| issue = 2
| journal = Journal of Combinatorial Theory, Series A
| mr = 1370138
| pages = 353–359
| title = Partitioning permutations into increasing and decreasing subsequences
| volume = 73
| year = 1996}}

{{cite OEIS|A029759}}

{{citation

| last = Stankova | first = Zvezdelina E. | authorlink = Zvezdelina Stankova
| doi = 10.1016/0012-365X(94)90242-9
| issue = 1-3
| journal = Discrete Mathematics
| mr = 1297387
| pages = 291–316
| title = Forbidden subsequences
| volume = 132
| year = 1994}}. See in particular Theorem 2.9, pp. 303–304.

1 : Permutation patterns

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。