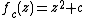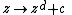- Definition
- Examples
Definition
In one-dimensional complex dynamics, the connectedness locus is a subset of the parameter space of rational functions, which consists of those parameters for which the corresponding Julia set is connected.
Examples
Without doubt, the most famous connectedness locus is the Mandelbrot set, which arises from the family of complex quadratic polynomials :
The connectedness loci of the higher-degree unicritical families,
(where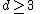 
) are often called 'Multibrot sets'.
For these families, the bifurcation locus is the boundary of the connectedness locus. This is no longer true in settings, such as the full parameter space of cubic polynomials, where there is more than one free critical point. For these families, even maps with disconnected Julia sets may display nontrivial dynamics. Hence here the connectedness locus is generally of less interest.
{{DEFAULTSORT:Connectedness Locus}}- Anzlom
- Anzoplana
- Anzoplanini
- Anzor Ashev
- Anzorey
- Anzorin
- Anzor Khizriev
- Anzor Sitchinava
- Anzor Urdia
- Anzovin, Steven
- ANZ Players Championship
- ANZ Premiership
- ANZ Stadium (Brisbane)
- ANZ Tasmanian International (tennis)
- ANZ Tour Championship
- Anzu (dinosaur)
- Anzu Haruno
- ANZUK Hospital
- Anzuman Ara Begum
- Anzum Ara Begum
- An Zuozhang
- Anzu Yamamoto
- Anzu Yumeno
- Anzy
- Anzá, Antioquia