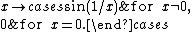- Darboux's theorem
- Proofs
- Darboux function
- Notes
- External links
In mathematics, Darboux's theorem is a theorem in real analysis, named after Jean Gaston Darboux. It states that every function that results from the differentiation of other functions has the intermediate value property: the image of an interval is also an interval.
When ƒ is continuously differentiable (ƒ in C1([a,b])), this is a consequence of the intermediate value theorem. But even when ƒ′ is not continuous, Darboux's theorem places a severe restriction on what it can be.
Darboux's theorem
Let  be a closed interval,
be a closed interval, 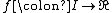 a real-valued differentiable function. Then
a real-valued differentiable function. Then  has the intermediate value property: If
has the intermediate value property: If  and
and  are points in
are points in  with
with  , then for every
, then for every  between
between 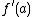 and
and 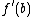 , there exists an
, there exists an  in
in  such that
such that 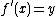 .[1][2][3]
.[1][2][3]
Proofs
Proof 1. The first proof is based on the extreme value theorem.
If  equals
equals 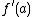 or
or 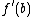 , then setting
, then setting  equal to
equal to  or
or  , respectively, gives the desired result. Now assume that
, respectively, gives the desired result. Now assume that  is strictly between
is strictly between 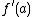 and
and 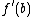 , and in particular that
, and in particular that 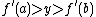 . Let
. Let 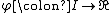 such that
such that 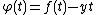 . If it is the case that
. If it is the case that 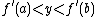 we adjust our below proof, instead asserting that
we adjust our below proof, instead asserting that  has its minimum on
has its minimum on  .
.
Since  is continuous on the closed interval
is continuous on the closed interval  , the maximum value of
, the maximum value of  on
on  is attained at some point in
is attained at some point in  , according to the extreme value theorem.
, according to the extreme value theorem.
Because 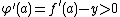 , we know
, we know  cannot attain its maximum value at
cannot attain its maximum value at  . (If it did, then
. (If it did, then 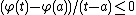 for all
for all 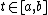 , which implies
, which implies 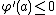 .)
.)
Likewise, because 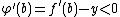 , we know
, we know  cannot attain its maximum value at
cannot attain its maximum value at  .
.
Therefore  must attain its maximum value at some point
must attain its maximum value at some point 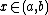 . Hence, by Fermat's theorem,
. Hence, by Fermat's theorem, 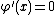 , i.e.
, i.e. 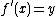 .
.
Define 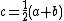 .
.
For 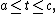 define
define 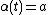 and
and 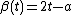 .
.
And for 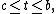 define
define 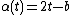 and
and 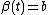 .
.
Thus, for 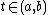 we have
we have 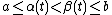 .
.
Now, define 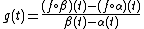 with
with 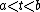 .
.
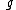 is continuous in
is continuous in  .
.
Furthermore, 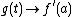 when
when 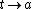 and
and 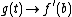 when
when 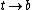 ; therefore, from the Intermediate Value Theorem, if
; therefore, from the Intermediate Value Theorem, if 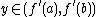 then, there exists
then, there exists 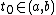 such that
such that 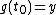 .
.
Let's fix  .
.
From the Mean Value Theorem, there exists a point 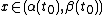 such that
such that 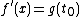 .
.
Hence, 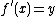 .
.
Darboux function
A Darboux function is a real-valued function ƒ which has the "intermediate value property": for any two values a and b in the domain of ƒ, and any y between ƒ(a) and ƒ(b), there is some c between a and b with ƒ(c) = y.[6] By the intermediate value theorem, every continuous function on a real interval is a Darboux function. Darboux's contribution was to show that there are discontinuous Darboux functions.
Every discontinuity of a Darboux function is essential, that is, at any point of discontinuity, at least one of the left hand and right hand limits does not exist.
An example of a Darboux function that is discontinuous at one point is the function
By Darboux's theorem, the derivative of any differentiable function is a Darboux function. In particular, the derivative of the function 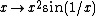 is a Darboux function even though it is not continuous at one point.
is a Darboux function even though it is not continuous at one point.
An example of a Darboux function that is nowhere continuous is the Conway base 13 function.
Darboux functions are a quite general class of functions. It turns out that any real-valued function ƒ on the real line can be written as the sum of two Darboux functions.[7] This implies in particular that the class of Darboux functions is not closed under addition.
A strongly Darboux function is one for which the image of every (non-empty) open interval is the whole real line. Such functions exist and are Darboux but nowhere continuous.[6]
Notes
2. ^Olsen, Lars: A New Proof of Darboux's Theorem, Vol. 111, No. 8 (Oct., 2004) (pp. 713–715), The American Mathematical Monthly
3. ^Rudin, Walter: Principles of Mathematical Analysis, 3rd edition, MacGraw-Hill, Inc. (1976), page 108
4. ^Apostol, Tom M.: Mathematical Analysis: A Modern Approach to Advanced Calculus, 2nd edition, Addison-Wesley Longman, Inc. (1974), page 112.
5. ^Olsen, Lars: A New Proof of Darboux's Theorem, Vol. 111, No. 8 (Oct., 2004) (pp. 713–715), The American Mathematical Monthly
6. ^1 {{cite book | last=Ciesielski | first=Krzysztof | title=Set theory for the working mathematician | zbl=0938.03067 | series=London Mathematical Society Student Texts | volume=39 | location=Cambridge | publisher=Cambridge University Press | year=1997 | isbn=0-521-59441-3 | pages=106–111 }}
7. ^Bruckner, Andrew M: Differentiation of real functions, 2 ed, page 6, American Mathematical Society, 1994
External links
- {{PlanetMath attribution|id=3055|title=Darboux's theorem}}
- {{springer|title=Darboux theorem|id=p/d030190}}
- John Ruan (disambiguation)
- John Ruane (director)
- John Rubel
- John Rubin
- John Rucho
- John Ruckdeschel
- John Rudd (basketball)
- John Ruddell
- John Ruddock
- John Rudey
- John Rudolph Sutermeister
- John Rudyerd
- John Rufus
- John Rufus Sharpe
- John Rufus Sharpe III
- John Ruganda
- John Rugee
- John Ruhl Sculptor
- John Ruhl (sculptor)
- John Ruiz vs. Roy Jones Jr.
- John Rumble
- John Rungsted Sørensen
- John Rusche
- John Ruscoe
- John Rusher