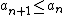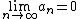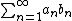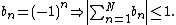“Dirichlet's test”的意思、由来-开放百科全书

词条

Dirichlet's test

释义

Statement
Proof
Applications
Improper integrals
Notes
References
External links

In mathematics, Dirichlet's test is a method of testing for the convergence of a series. It is named after its author Peter Gustav Lejeune Dirichlet, and was published posthumously in the Journal de Mathématiques Pures et Appliquées in 1862.^[1]

Statement

The test states that if 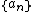is a sequence of real numbers and a sequence of complex numbers satisfying

for every positive integer N

where M is some constant, then the series

converges.

Proof

Let 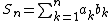and .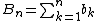

From summation by parts, we have that .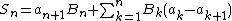

Since is bounded by M and , the first of these terms approaches zero, 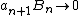as .

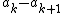On the other hand, since the sequence is decreasing, is non-negative for all k, so 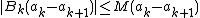. That is, the magnitude of the partial sum of , times a factor, is less than the upper bound of the partial sum (a value M) times that same factor.

But 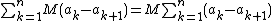, which is a telescoping sum that equals 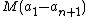and therefore approaches 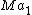as . Thus, 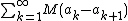converges.

In turn, 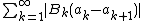converges as well by the Direct comparison test. The series 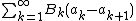converges, as well, by the absolute convergence test. Hence 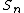converges.

Applications

A particular case of Dirichlet's test is the more commonly used alternating series test for the case

Another corollary is that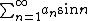

converges whenever 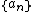is a decreasing sequence that tends to zero.

Moreover, Abel's test can be considered a special case of Dirichlet's test.

Improper integrals

An analogous statement for convergence of improper integrals is proven using integration by parts. If the integral of a function f is uniformly bounded over all intervals,

and g is a monotonically decreasing non-negative function, then the integral of fg is a convergent improper integral.

Notes

1. ^Démonstration d’un théorème d’Abel. Journal de mathématiques pures et appliquées 2nd series, tome 7 (1862), p. 253-255.

References

Hardy, G. H., A Course of Pure Mathematics, Ninth edition, Cambridge University Press, 1946. (pp. 379–380).
Voxman, William L., Advanced Calculus: An Introduction to Modern Analysis, Marcel Dekker, Inc., New York, 1981. (§8.B.13-15) {{ISBN|0-8247-6949-X}}.

External links

[https://web.archive.org/web/20060205051707/http://planetmath.org/encyclopedia/DirichletsConvergenceTest.html Proof at PlanetMath.org]

1 : Convergence tests

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。