三大几何作图问题sanda jihe zuotu wenti
古希腊的几何学家提出三个著名的几何作图问题:❶立方倍积问题(也叫做倍立方问题)——作一立方体,使其体积等于已知立方体体积的二倍;
❷三等分已知角问题——把已知角分成三个相等的部分;
❸化圆为方问题——作与已知圆等积的正方形.这三个问题的重要性在于:虽然用尺规能解很多的作图题,可是这三个问题却不能用尺规精确求解,而只能近似求解.对这三个问题的深入探索给希腊几何学以巨大的影响,并引出了大量的发现.例如,圆锥曲线、许多二次和三次曲线以及几种超越曲线的发现等;后来又有关于有理数域、代数数域和群论、方程论若干部分的发展.直到19世纪,即距第一次提出这三个问题的2千年之后,才从理论上证明了这三个问题不能用尺规作出.
伽罗华理论指出:若系数是有理数的三次方程没有有理根,则它的任何一个根,都不能从有理数体出发用圆规和直尺作出.根据这一理论可以证明前两个问题不能用尺规作出.第三个问题是林德曼在1882年证明π是超越数的同时证明的,现分别说明如下:
关于立方倍积问题,设已知立方体的棱长为a,所求立方体的棱长为x.由题意可知x3=2a3.此方程无有理根.所以不能用尺规作出.
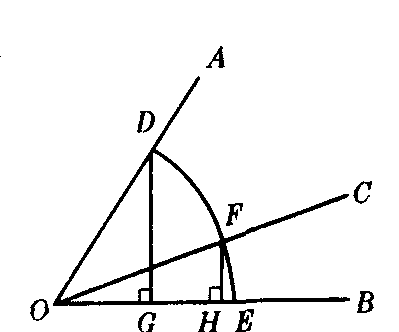
关于三等分已知角问题.如图,设OC是∠AOB的三等分线,以O为圆心,r为半径作弧和OA,OB,OC分别交于D,E,F,作DG⊥OB于G,FH⊥OB于H.设OG=a,OH=x,∠AOB=a,则cosa=
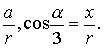
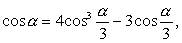
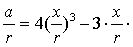
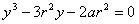
而±a,±r,±2a,±2r都不适合此方程.由(1)可知,方程是三次的,又没有有理根.所以用尺规不能三等分已知角.
关于化圆为方问题.设已知圆的半径为r.所求正方形的边长为x.依题意可知x
2=πr
2.即
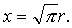
由于π是超越数,所以
也是超越数,不能用尺规作出.因此化圆为方问题不能用尺规作出.

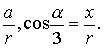
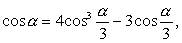
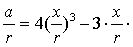
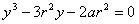 而±a,±r,±2a,±2r都不适合此方程.由(1)可知,方程是三次的,又没有有理根.所以用尺规不能三等分已知角.
而±a,±r,±2a,±2r都不适合此方程.由(1)可知,方程是三次的,又没有有理根.所以用尺规不能三等分已知角.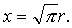 由于π是超越数,所以
由于π是超越数,所以 也是超越数,不能用尺规作出.因此化圆为方问题不能用尺规作出.
也是超越数,不能用尺规作出.因此化圆为方问题不能用尺规作出.