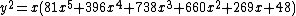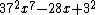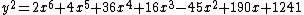“Elkies trinomial curves”的意思、由来-开放百科全书

词条

Elkies trinomial curves

释义

References

In number theory, the Elkies trinomial curves are certain hyperelliptic curves constructed by Noam Elkies which have the property that rational points on them correspond to trinomial polynomials giving an extension of Q with particular Galois groups.

One curve, C₁₆₈, gives Galois group PSL(2,7) from a polynomial of degree seven, and the other, C₁₃₄₄, gives Galois group AL(8), the semidirect product of a 2-elementary group of order eight acted on by PSL(2, 7), giving a transitive permutation subgroup of the symmetric group on eight roots of order 1344.

The equation of the curve C₁₆₈ is

The curve is a plane algebraic curve model for a Galois resolvent for the trinomial polynomial equation x⁷ + bx + c = 0. If there exists a point (x, y) on the (projectivized) curve, there is a corresponding pair (b, c) of rational numbers, such that the trinomial polynomial either factors or has Galois group PSL(2,7), the finite simple group of order 168. The curve has genus two, and so by Faltings theorem there are only a finite number of rational points on it. These rational points were proven by Nils Bruin using the computer program Kash to be the only ones on C₁₆₈, and they give only four distinct trinomial polynomials with Galois group PSL(2,7): x⁷-7x+3 (the Trinks polynomial), (1/11)x⁷-14x+3² (the Erbach-Fisher-McKay polynomial) and two new polynomials with Galois group PSL(2,7),

and

.

On the other hand, the equation of curve C₁₃₄₄ is

Once again the genus is two, and by Faltings theorem the list of rational points is finite. It is thought the only rational points on it correspond to polynomials x⁸+16x+28, x⁸+576x+1008, 19⁴53x⁸+19x+2 which have Galois group AL(8), and x⁸+324x+567, which comes from two different rational points and has Galois group PSL(2, 7) again, this time as the Galois group of a polynomial of degree eight.

References

{{cite conference

| author = Bruin, Nils; Elkies, Noam
| title = Trinomials ax⁷+bx+c and ax⁸+bx+c with Galois Groups of Order 168 and 8⋅168
| booktitle = Algorithmic Number Theory: 5th International Symposium, ANTS-V
| publisher = Lecture Notes in Computer Science, vol. 2369, Springer-Verlag
| year = 2002
| pages = 172–188
| mr = 2041082 }}

{{cite journal

|author1=Erbach, D. W. |author2=Fisher, J. |author3=McKay, J. | title = Polynomials with PSL(2,7) as Galois group
| journal = Journal of Number Theory
| volume = 11
| year = 1979
| issue = 1
| pages = 69–75
| mr = 0527761
| doi = 10.1016/0022-314X(79)90020-9}}

3 : Galois theory|Number theory|Algebraic curves

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。