三段论sanduanlun
传统逻辑主要推理之一。它是由两个包含着一个共同项的直言判断而推出一个新的直言判断的推理。亦称直言三段论。三段论共有三个不同的项（概念）:其中结论的主项叫小项，常用S表示；结论的谓项叫大项，常用P表示；两前提中共同包含的项叫中项，常用M表示。包含小项的前提叫小前提，包含大项的前提叫大前提。例如：
一切金属(M)都是能导电的(P),
铜(S)是金属(M),
所以，铜(M)是能导电的(P)。
三段论公理是三段论推理的依据。其内容是：一类事物的全部是什么（或不是什么），那么这类事物的部分也就是什么（或不是什么）。
三段论规则。要保证三段论是有效的，应遵守下列规则： （一）一个三段论中只能有三个不同的项。（二） M至少周延一次。（三）若S、P在前提中不周延，则在结论中不得周延。（四）两前提不能都是否定的。（五）若前提中有一个是否定的，则结论是否定的；若结论是否定的，则有一个前提是否定的。（六）两前提不能都是特称的。（七）若前提中有一个是特称的，则结论是特称的。
三段论的格。由中项M在两前提中的不同位置所决定的三段论形式。三段论有4个格：
各格的特征即特殊规则如下：第一格，小前提必肯定；大前提必全称。第二格，前提中总有一个是否定的；大前提必全称。第三格，小前提必肯定；结论必特称。第四格，若前提中有一否定，则大前提全称；若大前提肯定，则小前提全称；若小前提肯定，则结论特称；任何一个前提不能是O判断；结论不能是A判断。
三段论的式。A、E、I、O 4种判断在两个前提和结论中的各种不同组合形式。在传统逻辑中，三段论4个格共有24个有效式：
| 格 | 第1格 | 第2格 | 第3格 | 第4格 |
| 式 | AAA AAI AII EAE EAO EIO | AEE AEO AOO EAE EAO EIO | AAI AII EAO EIO IAI OAO | AAI AEE AEO EAO EIO IAI |
三段论的省略式。实际应用中的三段论常常是它的省略形式：或省略大前提，或省略小前提，或省略结论，亦称省略三段论。如“因为经济规律是客观规律，因此，它是不依人的意志为转移的”就是一个省略大前提“凡客观规律都是不依人的意志为转移的”的省略三段论。
三段论的复合式是若干三段论联结起来，并省略其中一些前提或结论的复杂推理形式。亦称复合三段论。主要有3种形式：❶前后三段论。其特点是前一个三段论的结论为后一个三段论前提之一。如所有C是D，所有B是C，所以，所有B是D；所有A是B，所以，所有A是D。
❷带证式。其特点是至少有一个前提本身是一个省略三段论。如所有B是D，因为所有B是C (省略所有C是D)；所有A是B，所以，所有A是D。
❸连锁推理。其特点是若干三段论联结起来，除最后的结论外，其他结论均被省略，并且每两个相邻的判断都有一共同项。如亚里士多德式（后退式）:所有A是B，所有B是C，所有C是D，所以，所有A是D。哥克兰尼式（前进式）:所有C是D，所有B是C，所有A是B，所以，所有A是D。
现代逻辑考虑到三段论的词项可以是空类，因此9个由两全称前提得出特称结论的三段论在现代逻辑中是无效的。
三段论san duan lun
亦称三段论法.是以两个（含有一个共同项的）性质判断作为前提，根据一定的推理规则（正确推理形式），推出一个性质判断作为结论的演绎推理.例如，下式就是三段论法的一个公式：
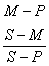
所有的平行四边形(M)都是对角相等的四边形(P),
所有的菱形(S)都是平行四边形，
所以，所有的菱形(S)都是对角相等的四边形(P).
三段论的根据是三段论的公理：凡对一类事物有所肯定，则对该类事物中的每一分子也应有所肯定；凡对一类事物有所否定，则对该类事物中的每一分子也应有所否定.三段论公理也可用概念的外延——集合来说明.图1表示：S⊆M,M⊆P，所以，S⊆P.图2表示：M∩P=Φ,S⊆M，所以S∩P=Φ.
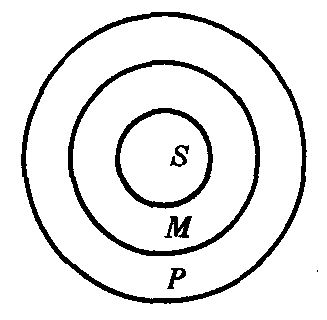
图1
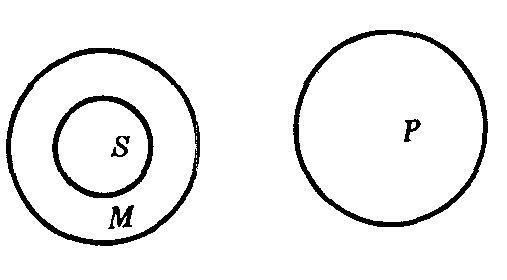
图2
三段论是中学数学中最为常用的一种演绎推理.它所以重要，是因为它被用于数学证明.
三段论Sanduanlun
三段论是由两个包含着一个共同项的性质判断而推出一个新的性质判断的推理，逻辑中习惯称为三段论（又称直言三段论）。如：凡物质都是运动的，太阳是物质，所以，太阳是运动的。任何一个三段论都是由三个性质判断组成， 两个是前提，一个是结论。任何一个三段论都包含三个项：小项、大项与中项。结论中的主项叫小项， 如前例中的 “太阳”；结论中的谓项叫大项，如前例中的“运动的”；两个前提中所共有的项叫中项，如前例中的“物质”。在两个前提中，具有大项的前提叫大前提，如前例中的“凡物质都是运动的”；具有小项的前提叫小前提，如前例中的 “太阳是物质”。三段论是由两个判断向一个新判断的过渡。其所以能过渡，是因为它是以三段论公理为依据的。三段论的公理是：一类事物的全部是什么或不是什么，那么这类事物中的部分也是什么或不是什么。换句话说，如果对一类事物的全部有所断定，那么对它的部分也就有所断定。三段论推理必须遵守以下几条规则， 这些规则是判定一个三段论推理是否正确的标准。这些规则是：❶在一个三段论中，只能有三个不同的项。三段论中如果出现四个项，就叫做“四项错误”，或叫“四名词错误”。
❷中项在前提中至少要周延一次。两个中项都不周延，就叫做“中项不周延的错误”。
❸在前提中不周延的项，在结论中也不得周延。违反这条规则，大项在前提中不周延而在结论中周延，就叫做“大项扩大的错误，” 小项在前提中不周延而在结论中周延，就叫做“小项扩大的错误”。
❹从两个否定的前提不能得出结论。否定判断所确定的是主、谓项相互排斥，如果两前提都是否定的，则所确定的是大、小项都和中项排斥。这样，中项就起不到联结大、小项的作用，从而也就不能确定大、小项之间的关系。所以，从两个否定前提不能必然地得出结论。
❺两个前提中如果有一个是否定的，则结论是否定的；如果结论是否定的，则必有一个前提是否定的。
❻从两个特称的前提不能得出结论。
❼如果有一个前提是特称的，只能得出特称的结论。三段论有四个格。三段论的格是由中项在两个前提中的位置不同所决定的三段论的形式。三段论的四个格是：第一格：中项在大前提中是主项，在小前提中是谓项。第二格：中项在两个前提中都是谓项。第三格：中项在两个前提中都是主项。第四格：中项在大前提中是谓项， 在小前提中是主项。各格有各格的规则。第一格的规则是：小前提必肯定；大前提必全称。第二格的规则是：两前提中必有一个是否定的；大前提必全称。第三格的规则是：小前提必肯定；结论必特称。第四格的规则是：如两个前提有一个否定，则大前提全称；如大前提肯定，则小前提全称；如小前提肯定，则结论特称；任何一个前提都不能是特称否定；结论不能是全称肯定判断。三段论也有不同的式，三段论的式是由于前提和结论的质、量的不同而形成的不同形式的三段论，三段论共有十九个正确的式。
三段论
又称“直言三段论”。为古希腊哲学家亚里士多德所创。由两个包含着一个共同词项的直言判断推出一个新的直言判断的间接推理。如“物质形态都是有内部结构的；基本粒子都是物质形态。所以，基本粒子也都是有内部结构的”。三段论是传统逻辑的重要内容。